如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙 、
、 的夹角为
的夹角为 (即
(即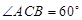 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 
设数列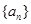 的前
的前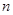 项和
项和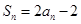 .数列
.数列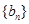 满足:
满足: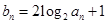 .
.
(1)求 的通项
的通项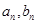 .并比较
.并比较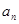 与
与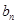 的大小;
的大小;
(2)求证: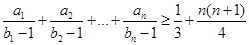 .
.
已知椭圆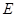 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在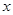 轴上,离心率为
轴上,离心率为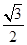 ,且过双曲线
,且过双曲线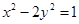 的顶点.
的顶点.
(1)求椭圆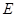 的标准方程;
的标准方程;
(2)命题:“设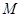 、
、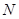 是双曲线
是双曲线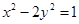 上关于它的中心对称的任意两点,
上关于它的中心对称的任意两点,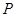 为该双曲线上的动点,若直线
为该双曲线上的动点,若直线 、
、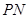 均存在斜率,则它们的斜率之积为定值”.试类比上述命题,写出一个关于椭圆
均存在斜率,则它们的斜率之积为定值”.试类比上述命题,写出一个关于椭圆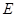 的类似的正确命题,并加以证明和求出此定值;
的类似的正确命题,并加以证明和求出此定值;
(3)试推广(Ⅱ)中的命题,写出关于方程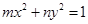 (
(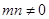 ,
,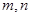 不同时为负数)的曲线的统一的一般性命题(不必证明).
不同时为负数)的曲线的统一的一般性命题(不必证明).
设函数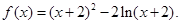
(1)求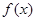 的单调区间;
的单调区间;
(2)若关于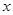 的方程
的方程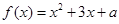 在区间
在区间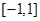 上有唯一实根,求实数
上有唯一实根,求实数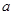 的取值范围.
的取值范围.
已知等差数列 满足:
满足: ,
, ,
, 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)令 =
= (
( ),求数列
),求数列 的前
的前 项和
项和 .
.
(1)已知函数 在某一个周期内的图象的最高点和最低点的坐标分别为
在某一个周期内的图象的最高点和最低点的坐标分别为 ,
, .
.
求 和
和 的值;
的值;
(2)已知 ,且
,且 , 求
, 求 的值.
的值.