某种波的传播是由曲线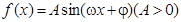 来实现的,我们把函数解析式
来实现的,我们把函数解析式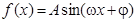 称为“波”,把振幅都是A 的波称为“ A 类波”,把两个解析式相加称为波的叠加.
称为“波”,把振幅都是A 的波称为“ A 类波”,把两个解析式相加称为波的叠加.
(1)已知“1 类波”中的两个波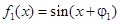 与
与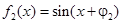 叠加后仍是“1类波”,求
叠加后仍是“1类波”,求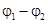 的值;
的值;
(2)在“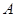 类波“中有一个波是
类波“中有一个波是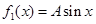 ,从
,从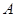 类波中再找出两个不同的波(每两个波的初相
类波中再找出两个不同的波(每两个波的初相 都不同),使得这三个不同的波叠加之后是平波,即叠加后是
都不同),使得这三个不同的波叠加之后是平波,即叠加后是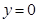 ,并说明理由.
,并说明理由.
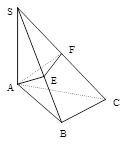
如右图所示,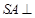 平面ABC,
平面ABC,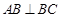 ,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证:⑴
,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证:⑴ ;⑵
;⑵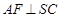 .
.
某地植被面积  (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数 (
( )之间有如下的对应数据:
)之间有如下的对应数据:
 (公顷) (公顷) |
20 |
40 |
50 |
60 |
80 |
 ( ( ) ) |
3 |
4 |
4 |
4 |
5 |
⑴ 请用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
⑵ 根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少 ?
?
参考公式:
用最小二乘法求线性回归方程系数公式: .
.
已知 ,
,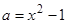 ,
,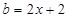 。求证
。求证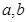 中至少有一个不小于0。
中至少有一个不小于0。
某校在两个班进行教学方式对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如 列联表所示(单位:人).
列联表所示(单位:人).
⑴ 求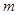 ,
,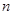 ;
;
⑵ 你有多大把握认为“教学方式与成绩有关系”?
| 80及80分以上 |
80分以下 |
合计 |
|
| 试验班 |
35 |
15 |
50 |
| 对照班 |
20 |
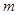 |
50 |
| 合计 |
55 |
45 |
 |
参考公式及数据: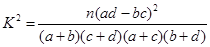 ,其中
,其中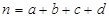 为样本容量.
为样本容量.
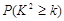 |
… |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
… |
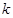 |
… |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
… |
已知数列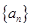 的前
的前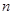 项和
项和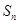 满足
满足 ,且
,且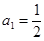 .
.
⑴ 求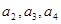 的值;
的值;
⑵ 猜想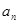 的表达式(不必证明)
的表达式(不必证明)