已知圆C：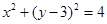
，一动直线
过A（-1，0）与圆C相交于P、Q两点，M是PQ的中点，与直线m：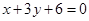
相交于N．
（1）求证：当与m垂直时，必过圆心C；
（2）当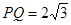
时，求直线的方程；
（3）探索向量AM与向量AN，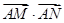
是否与直线的倾斜角有关，若无关，请求出其值；若有关，请说明理由。
设函数
，若
在
处有极值
（1）求实数
的值
（2）求函数
的极值
（3）若对任意的
，都有
，求实数
的取值范围
分别求适合下列条件的圆锥曲线的标准方程：
（1）离心率为
，焦点坐标为
和
的双曲线
（2）离心率
，准线方程为
的椭圆
（3）焦点在
轴的正半轴上，焦点到准线的距离为4的抛物线
已知等差数列
满足
（1）求数列的通项公式
（2）若数列的前n项和为
，求
（本小题满分10分）（1）设
，试比较
与
的大小；
（2）是否存在常数
，使得
对任意大于
的自然数
都成立？若存在，试求出
的值并证明你的结论；若不存在，请说明理由．
已知从“神州”飞船带回的某种植物种子每粒成功发芽的概率都为
，某植物研究所进行该种子的发芽实验，每次实验种一粒种子，每次实验结果相互独立，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败.若该研究所共进行四次实验，设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
（1）求随机变量ξ的数学期望E(ξ)；
（2）记“函数f(x)= x2－
x-1在区间（2，3）上有且只有一个零点”为事件A，求事件A发生的概率P（A）．