(本小题满分13分)函数 部分图象如图所示.
部分图象如图所示.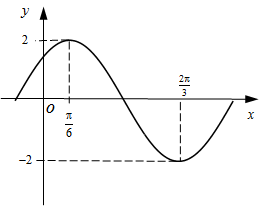
(Ⅰ)求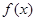 的最小正周期及解析式;
的最小正周期及解析式;
(Ⅱ)设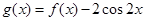 ,求函数
,求函数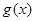 在区间
在区间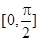 上的最大值和最小值.
上的最大值和最小值.
(本小题满分13分)已知在等比数列 中,
中, ,且
,且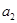 是
是 和
和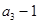 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列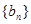 满足
满足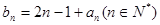 ,求
,求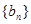 的前
的前 项和
项和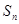 .
.
(本小题满分14分)给定数列 .对
.对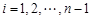 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后 项
项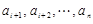 的最小值记为
的最小值记为 ,
,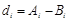 .
.
(Ⅰ)设数列 为
为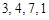 ,写出
,写出 ,
, ,
, 的值;
的值;
(Ⅱ)设 (
( )是公比大于
)是公比大于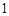 的等比数列,且
的等比数列,且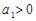 .证明:
.证明: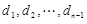 是等比数列;
是等比数列;
(Ⅲ)设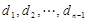 是公差大于
是公差大于 的等差数列,且
的等差数列,且 .证明:
.证明: 是等差数列.
是等差数列.
(本小题满分14分)已知函数 .
.
(Ⅰ)当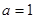 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数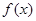 的单调区间;
的单调区间;
(Ⅲ)若对任意 ,
, ,且
,且 恒成立,求
恒成立,求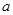 的取值范围.
的取值范围.
(本小题满分13分)如图,港口 在港口
在港口 正东方
正东方 海里处,小岛
海里处,小岛 在港口
在港口 北偏东
北偏东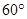 方向和港口
方向和港口 北偏西
北偏西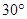 方向上,一艘科学考察船从港口O出发,沿北偏东
方向上,一艘科学考察船从港口O出发,沿北偏东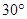 的
的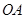 方向以每小时
方向以每小时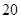 海里的速度驶离港口
海里的速度驶离港口 ,一艘快艇从港口B出发,以每小时
,一艘快艇从港口B出发,以每小时 海里的速度驶向小岛
海里的速度驶向小岛 ,在
,在 岛装运补给物资后给考察船送去,现两船同时出发,补给物资的装船时间需要
岛装运补给物资后给考察船送去,现两船同时出发,补给物资的装船时间需要 小时,问快艇驶离港口
小时,问快艇驶离港口 后最少要经过多少时间才能和考察船相遇?
后最少要经过多少时间才能和考察船相遇?