已知抛物线 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,与圆
两点,与圆 交于
交于 两点,当
两点,当 时,求
时,求 的取值范围.
的取值范围.
如图,矩形 所在的平面和平面
所在的平面和平面 互相垂直,等腰梯形
互相垂直,等腰梯形 中,
中, ,分别为
,分别为 的中点,
的中点, 为底面
为底面 的重心.
的重心.
(1)求证: ;
;
(2)求证: .
.
甲、乙两位同学从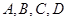 共四所高校中,任选两所参加自主招生考试(并且只能选两所高校),但同学甲特别喜欢
共四所高校中,任选两所参加自主招生考试(并且只能选两所高校),但同学甲特别喜欢 高校,他除选
高校,他除选 高校外,再会在余下的3所中随机选1所;同学乙对4所高校没有偏爱,在4所高校中随机选2所.
高校外,再会在余下的3所中随机选1所;同学乙对4所高校没有偏爱,在4所高校中随机选2所.
(1)求乙同学选中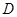 高校的概率;
高校的概率;
(2)求甲、乙两名同学恰有一人选中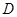 高校的概率.
高校的概率.
已知数列 的前
的前 项和为
项和为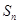 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设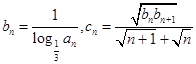 ,求数列
,求数列 的前
的前 项和
项和 .
.
选修4 - 4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线 的极坐标方程为
的极坐标方程为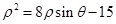 ,曲线
,曲线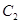 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)将 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若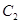 上的点
上的点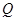 对应的参数为
对应的参数为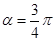 ,
,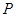 为
为 上的动点,求
上的动点,求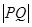 的最小值。
的最小值。