(本小题满分12分)某学校1800名学生在一次一百米测试中,全部介于13秒与18秒之间,抽取其中的50个样本,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组 ,第三组
,第三组 ,…,第五组
,…,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于15秒认为良好,求该样本在这在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数与平均数;
(4)请根据频率分布直方图,求样本数据的中位数.(保留两小数)
某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系,随机抽取了100名员工进行调查,其中支持企业改革的调查者中,工作积极的46人,工作一般的35人,而不太赞成企业改革的调查者中,工作积极的4人,工作一般的15人.
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)对于人力资源部的研究项目,根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系?
参考公式: (其中
(其中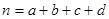 )
)
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知复数 满足
满足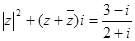 (i为虚数单位),求
(i为虚数单位),求 。
。
已知函数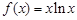 .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)若对所有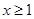 都有
都有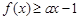 ,求实数
,求实数 的取值范围.
的取值范围.
如图所示,已知直四棱柱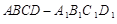 中,
中,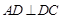 ,
, ,且满足
,且满足 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.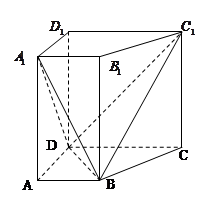
已知点P(3,4)是椭圆+=1(a>b>0)上的一点,F1、F2是椭圆的两焦点,若PF1⊥PF2,试求:
(1)椭圆方程;
(2)△PF1F2的面积.