(本题满分14分,第(1)小题6分,第(2)小题8分)
如图,在四棱锥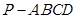 中,底面
中,底面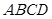 为矩形,
为矩形, 平面
平面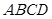 ,点
,点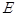 在线段
在线段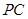 上,
上,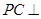 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,
, ,求二面角
,求二面角 的大小.
的大小.
(本题满分12分) 已知函数 的定义域为
的定义域为 .
.
(Ⅰ)求集合 ;
;
(Ⅱ)若函数 ,且
,且 ,求函数
,求函数 的最大最小值和对应的
的最大最小值和对应的 值;
值;
(本题满 分12分) 设
分12分) 设 ,
, 其中
其中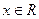 ,
,
如果 ,求实数
,求实数 的取值范围.
的取值范围.
(本题满分12分)
(Ⅰ)从 名男生和
名男生和 名女生中任选
名女生中任选 人去参加培训,用
人去参加培训,用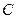 表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件
表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件 的对立事件,并求事件
的对立事件,并求事件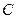 的概率;
的概率;
(Ⅱ)函数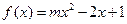 ,那么任意
,那么任意 ,使函数
,使函数 在实数集上有零根的概率.
在实数集上有零根的概率.
(本题满分12分)
某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图, 其中身高的变化范围是 (单位:厘米),样本数据分组为
(单位:厘米),样本数据分组为 ,
,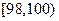 ,
,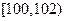 ,
,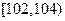 ,
,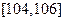 ,
,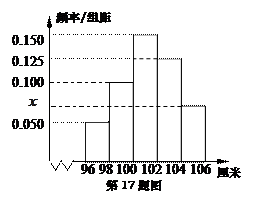
(Ⅰ)求出 的值;
的值;
(Ⅱ)已知样本中身高小于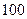 厘米的人数是
厘米的人数是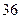 ,求出样本总量
,求出样本总量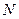 的数值;
的数值;
(Ⅲ)根据频率分布直方图提供的数据,求出样本中身高大于或等于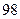 厘米并且小于
厘米并且小于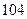 厘米学生数.
厘米学生数.
(12分)如图,在四棱锥P-ABCD中,底面
ABCD是矩形,PA⊥平面ABCD,AP=AB,
BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求四棱锥E-ABCD的体积V;
(Ⅲ)求二面角E-AD-C的大小.
 |