已知抛物线y=-mx2+4x+2m与x轴交于点A(α,0), B(β,0),且 .
.
(1)求抛物线的解析式.
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E.是否存在x轴上的点M、y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.
已知,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.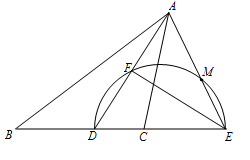
(1)判断AF与DF的数量关系,并说明理由;
(2)只用无刻度的直尺画出△ADE的边DE上的高AH;
(3)若EF=4,DF=3,求DH的长.
水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60º,将菱形OABC绕坐标原点O逆时针旋转120º得到菱形ODEF.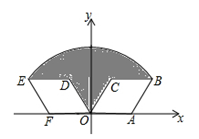
(1)直接写出点F的坐标;
(2)求线段OB的长及图中阴影部分的面积.
如图,四边形ABCD为菱形,M为BC上一点,连接AM,交对角线BD于点G,并且∠ABM=2∠BAM.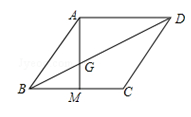
(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求△ADG的面积.
已知关于x的一元二次方程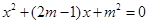 有两个实数根
有两个实数根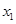 、
、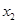 ,并且满足
,并且满足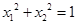 ,求m的值.
,求m的值.