已知,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.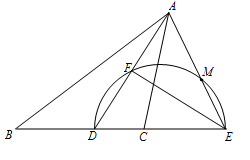
(1)判断AF与DF的数量关系,并说明理由;
(2)只用无刻度的直尺画出△ADE的边DE上的高AH;
(3)若EF=4,DF=3,求DH的长.
如图所示,在四边形ABCD中,∠A=80°,∠C=75°,∠ADE为四边形ABCD的一个外角,且∠ADE=125°,试求出∠B的度数.
如图,△ABC中,AB="AC," ∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,
(1)求∠ACB的度数;
(2)HE= AF
AF
如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。
已知∠MAN,AC平分∠MAN.
(1)在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.
(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.