(本小题满分12分)已知椭圆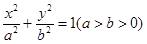 上任意一点到两焦点
上任意一点到两焦点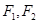 距离之和为
距离之和为 ,离心率为
,离心率为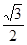 .
.
(1)求椭圆的标准方程;
(2)若直线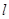 的斜率为
的斜率为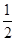 ,直线
,直线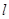 与椭圆C交于
与椭圆C交于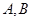 两点.点
两点.点 为椭圆上一点,求△PAB的面积的最大值.
为椭圆上一点,求△PAB的面积的最大值.
某中学对高二甲、乙两个同类班级进行加强语文阅读理解训练对提高数学应用题得分率作用的试验,其中甲班为实验班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用试题测试的平均成绩(均取整数)如表所示:
| 60分以下 |
61﹣70分 |
71﹣80分 |
81﹣90分 |
91﹣100分 |
|
| 甲班(人数) |
3 |
6 |
11 |
18 |
12 |
| 乙班(人数) |
3 |
9 |
13 |
15 |
10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)试分析估计两个班级的优秀率;
(2)由以上统计列出2×2列联表.
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)用x的代数式表示AM,并写出x的取值范围;
(2)求S关于x的函数关系式.
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项与偶数项各有什么特点?并加以说明.
已知椭圆的顶点与双曲线 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在y轴上.
,若椭圆的焦点在y轴上.
(1)求双曲线的离心率,并写出其渐近线方程;
(2)求椭圆的标准方程.
已知函数f(x)=﹣ x3+x2+3x+a.
x3+x2+3x+a.
(1)求f(x)的单调区间;
(2)若f(x)在区间[﹣3,3]上的最小值为 ,求a的值.
,求a的值.