(本小题满分10分)选修4—1:几何证明选讲
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和圆O分别交于点D和E.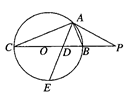
(1)求证: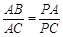 ;
;
(2)求AD·AE的值.
已知函数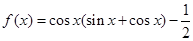
(1)若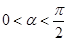 ,且
,且 ,求
,求 的值;
的值;
(2)求函数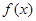 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
(Ⅰ)求直线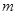 :
: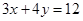 与两坐标轴所围成的三角形的内切圆
与两坐标轴所围成的三角形的内切圆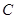 的方程;
的方程;
(Ⅱ)若与(Ⅰ)中的圆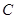 相切的直线
相切的直线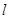 交
交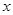 轴
轴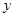 轴于
轴于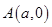 和
和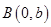 两点,且
两点,且 .
.
①求证:圆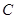 与直线
与直线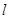 相切的条件为
相切的条件为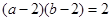 ;
;
②求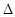 OAB面积的最小值及此时直线
OAB面积的最小值及此时直线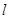 的方程.
的方程.
(本小题满分14分)已知两圆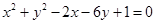 和
和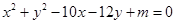
(1)m取何值时,两圆外切;
(2)m取何值时,两圆内切;
(3)求m=45时两圆的公共弦所在直线的方程和公共弦的长.
已知圆C经过A(3,2),B(1,6)圆心在直线y=2x上。
(1)求圆C方程;(2)若直线 x+2y+m=0与圆C相交于M、N两点,且∠MAN=600,求m的值。
已知直线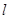 经过直线
经过直线 与直线
与直线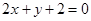 的交点
的交点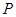 ,且垂直于直线
,且垂直于直线 .
.
(1)求直线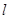 的方程;
的方程;
(2)求直线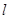 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积 .
.