(本小题满分14分)已知两圆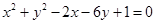 和
和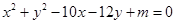
(1)m取何值时,两圆外切;
(2)m取何值时,两圆内切;
(3)求m=45时两圆的公共弦所在直线的方程和公共弦的长.
已知函数 的定义域为
的定义域为 ,且
,且 ,
, ,
,
当 ,
,
 且
且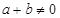 ,时
,时 恒成立.
恒成立.
(1)判断 在
在 上的单调性;
上的单调性;
(2)解不等式 ;
;
(3)若 对于所有
对于所有 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知点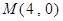 、
、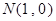 ,若动点
,若动点 满足
满足 .
.
(1)求动点 的轨迹曲线
的轨迹曲线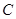 的方程;
的方程;
(2)在曲线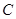 上求一点
上求一点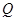 ,使点
,使点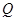 到直线:
到直线: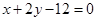 的距离最小.
的距离最小.
在如图所示的几何体中,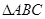 是边长为
是边长为 的正三角形,
的正三角形, ,
, 平面
平面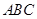 ,平面
,平面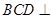 平面
平面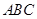 ,
,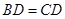 ,且
,且 .
.
(1)证明: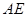 //平面
//平面 ;
;
(2)证明:平面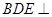 平面
平面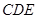 ;
;
(3)求该几何体的体积.
甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的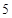 次预赛成绩记录如下:
次预赛成绩记录如下:
甲

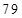

 乙
乙



(1)用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)①求甲、乙两人的成绩的平均数与方差,②若现要从中选派一人参加数学竞赛,
根据你的计算结果,你认为选派哪位学生参加合适?
已知向量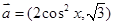 ,
, ,函数
,函数 .
.
(1)求函数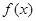 的最小正周期;
的最小正周期;
(2)若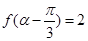 ,
,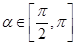 ,求
,求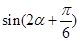 的值.
的值.