(本小题满分12分)已知在直角坐标系xoy中,曲线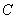 的参数方程为
的参数方程为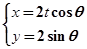
(t为非零常数,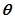 为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以
为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数 ,使得直线
,使得直线 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点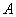 、
、 ,且
,且
(其中o为坐标原点)?若存在,请求出;否则,请说明理由
已知集合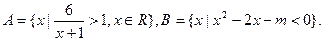
(1)当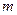 =3时,求
=3时,求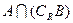 ;
;
(2)若 ,求实数
,求实数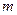 的值.
的值.
一边长为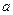 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为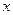 的
的 小正方形,然后做成一个无盖方盒.(1)将方盒的容积表示成
小正方形,然后做成一个无盖方盒.(1)将方盒的容积表示成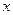 的函数
的函数 ;(2)当
;(2)当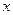 是多少时,方盒的容积最大?最大容积是多少?
是多少时,方盒的容积最大?最大容积是多少?
已知数列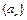 中,
中,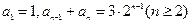 .
.
(1)求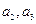 ;(2)求
;(2)求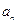 的通项公式;(3)证明:
的通项公式;(3)证明: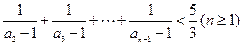

一动圆 与圆
与圆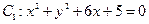 外切,同时与圆
外切,同时与圆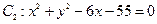 内切.
内切.
(1)求动圆圆心 的轨迹
的轨迹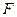 的方程;
的方程;
(2)在矩形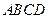 中(如图),
中(如图),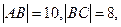
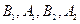 分别是矩形四边的中点,
分别是矩形四边的中点,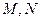 分别是
分别是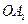 (其中
(其中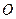 是坐标系原点)
是坐标系原点)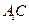 的中点,直线
的中点,直线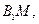
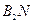 的交点为
的交点为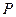 ,证明点
,证明点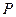 在轨迹
在轨迹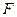 上.
上.
如图:
在棱长为1的正方体 —
— 中.
中.
点M是棱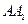 的中点,点
的中点,点 是
是 的中点.
的中点.
(1)求证: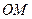 垂直于平面
垂直于平面 ;
;
(2)求平面 与平面
与平面 所成二面角的平面角(锐角)
所成二面角的平面角(锐角)
的余弦值.