某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．已知两组技工在单位时间内加工的合格零件平均数都为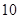
．
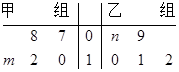
（1）分别求出
，
的值；
（2）分别求出甲、乙两组技工在单位时间内加工的合格零件的方差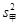
和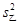
，并由此分析两组技工的加工水平；
（3）质检部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，若两人加工的合格零件个数之和大于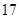
，则称该车间“质量合格”，求该车间“质量合格”的概率．
（注：方差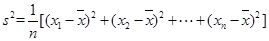
，其中
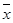为数据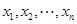
的平均数）．
已知全集
集合
，
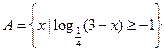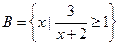，求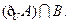
设
（1）若
且对任意实数
均有
成立，求
的表达式；
（2）在（1）条件下，当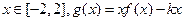
是单调递增，求实数k的取值范围。
已知函数
在区间[0，1]上单调递增，在区间[1，2]上单调递减。（1）求实数
的值.（2）设
，关于
的方程
的解集恰有3个元素，求实数
的取值范围。
如图四棱锥P-ABCD中，底面ABCD为矩形，PA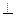
底面ABCD，PA=AB=
，点E是棱PB的中点。（1）求直线AD与平面PBC的距离。
（2）若AD=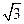
，求二面角A-EC-D的平面角的余弦值。
甲、乙两人独立解出某一道数学题的概率相同。已知该题被甲或乙解出的概率为0.36。求：（I）甲独立解出该题的概率。（II）恰有1人解出该题的概率。