(本小题满分10分)选修4-1:几何证明选讲
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
【2015高考福建,理20】已知函数 ,
,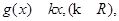
(Ⅰ)证明:当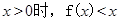 ;
;
(Ⅱ)证明:当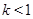 时,存在
时,存在 ,使得对
,使得对
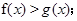
(Ⅲ)确定k的所以可能取值,使得存在 ,对任意的
,对任意的 恒有
恒有 .
.
【2015高考江苏,19】(本小题满分16分)已知函数 .
.
(1)试讨论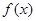 的单调性;
的单调性;
(2)若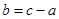 (实数c是a与无关的常数),当函数
(实数c是a与无关的常数),当函数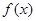 有三个不同的零点时,a的取值范围恰好是
有三个不同的零点时,a的取值范围恰好是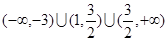 ,求c的值.
,求c的值.
【2015高考新课标2,理21】
设函数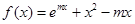 .
.
(Ⅰ)证明: 在
在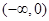 单调递减,在
单调递减,在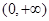 单调递增;
单调递增;
(Ⅱ)若对于任意 ,都有
,都有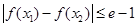 ,求
,求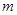 的取值范围.
的取值范围.
【2015高考上海,理23】对于定义域为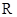 的函数
的函数 ,若存在正常数
,若存在正常数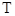 ,使得
,使得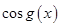 是以
是以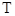 为周期的函数,则称
为周期的函数,则称 为余弦周期函数,且称
为余弦周期函数,且称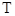 为其余弦周期.已知
为其余弦周期.已知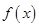 是以
是以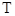 为余弦周期的余弦周期函数,其值域为
为余弦周期的余弦周期函数,其值域为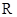 .设
.设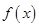 单调递增,
单调递增, ,
, .
.
(1)验证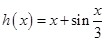 是以
是以 为周期的余弦周期函数;
为周期的余弦周期函数;
(2)设 .证明对任意
.证明对任意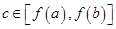 ,存在
,存在 ,使得
,使得 ;
;
(3)证明:“ 为方程
为方程 在
在 上得解”的充要条件是“
上得解”的充要条件是“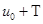 为方程
为方程 在
在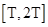 上有解”,并证明对任意
上有解”,并证明对任意 都有
都有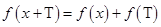 .
.
【2015高考北京,理20】已知数列 满足:
满足: ,
, ,且
,且
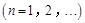 .
.
记集合 .
.
(Ⅰ)若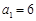 ,写出集合
,写出集合 的所有元素;
的所有元素;
(Ⅱ)若集合 存在一个元素是3的倍数,证明:
存在一个元素是3的倍数,证明: 的所有元素都是3的倍数;
的所有元素都是3的倍数;
(Ⅲ)求集合 的元素个数的最大值.
的元素个数的最大值.