如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连-优题课

如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．
可证：AE⊥BF；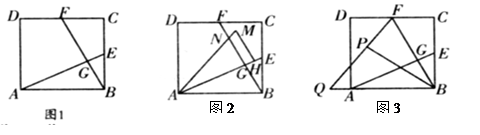

（1）将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM，如图2，若AM和BF相交
于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．
（2）将△BCF沿BF对折，得到△BPF，如图3，延长FP交BA的延长线于点Q，求sin∠BQP的值；

科目数学题型解答题难度较难

知识点：圆内接四边形的性质相似多边形的性质对称式和轮换对称式解直角三角形

已知如图，在平面直角坐标系 $xOy$ 中，点 $A$ 、 $B$ 、 $C$ 分别为坐标轴上的三个点，且 $OA = 1$ ， $OB = 3$ ， $OC = 4$ ，

（1）求经过 $A$ 、 $B$ 、 $C$ 三点的抛物线的解析式；

（2）在平面直角坐标系 $xOy$ 中是否存在一点 $P$ ，使得以点 $A$ 、 $B$ 、 $C$ 、 $P$ 为顶点的四边形为菱形？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由；

（3）若点 $M$ 为该抛物线上一动点，在（2）的条件下，请求出当 $| PM - AM |$ 的最大值时点 $M$ 的坐标，并直接写出 $| PM - AM |$ 的最大值．

如图， $ΔABC$ 和 $ΔBEC$ 均为等腰直角三角形，且 $∠ ACB = ∠ BEC = 90 °$ ， $AC = 4 \sqrt{2}$ ，点 $P$ 为线段 $BE$ 延长线上一点，连接 $CP$ 以 $CP$ 为直角边向下作等腰直角 $ΔCPD$ ，线段 $BE$ 与 $CD$ 相交于点 $F$

（1）求证： $\frac{PC}{CD} = \frac{CE}{CB}$ ；

（2）连接 $BD$ ，请你判断 $AC$ 与 $BD$ 有什么位置关系？并说明理由；

（3）设 $PE = x$ ， $ΔPBD$ 的面积为 $S$ ，求 $S$ 与 $x$ 之间的函数关系式．

“世界那么大，我想去看看”一句话红遍网络，骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场．顺风车行经营的 $A$ 型车去年6月份销售总额为3.2万元，今年经过改造升级后 $A$ 型车每辆销售价比去年增加400元，若今年6月份与去年6月份卖出的 $A$ 型车数量相同，则今年6月份 $A$ 型车销售总额将比去年6月份销售总额增加 $25 %$ ．

（1）求今年6月份 $A$ 型车每辆销售价多少元（用列方程的方法解答）；

（2）该车行计划7月份新进一批 $A$ 型车和 $B$ 型车共50辆，且 $B$ 型车的进货数量不超过 $A$ 型车数量的两倍，应如何进货才能使这批车获利最多？

$A$ 、 $B$ 两种型号车的进货和销售价格如表：

	$A$ 型车	$B$ 型车
进货价格（元 $/$ 辆）	1100	1400
销售价格（元 $/$ 辆）	今年的销售价格	2400

九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识，在三张完全相同且不透明的卡片正面分别写上了 $- 3$ ，0，2三个数字，背面向上洗匀后随机抽取一张，将卡片上的数字记为 $a$ ，再从剩下的两张中随机取出一张，将卡片上的数字记为 $b$ ，然后叫万宇在平面直角坐标系中找出点 $M (a, b)$ 的位置．

（1）请你用树状图帮万宇同学进行分析，并写出点 $M$ 所有可能的坐标；

（2）求点 $M$ 在第二象限的概率；

（3）张老师在万宇同学所画的平面直角坐标系中，画了一个半径为3的 $⊙ O$ ，过点 $M$ 能作多少条 $⊙ O$ 的切线？请直接写出答案．

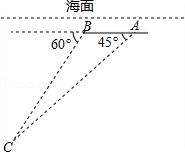
如图，埃航 $MS 804$ 客机失事后，国家主席亲自发电进行慰问，埃及政府出动了多艘舰船和飞机进行搜救，其中一艘潜艇在海面下500米的 $A$ 点处测得俯角为 $45 °$ 的前下方海底有黑匣子信号发出，继续沿原方向直线航行2000米后到达 $B$ 点，在 $B$ 处测得俯角为 $60 °$ 的前下方海底有黑匣子信号发出，求海底黑匣子 $C$ 点距离海面的深度（结果保留根号）．