(年贵州六盘水14分)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ,)
,)
(年广东佛山11分)我们把“按照某种理想化的要求(或实际可能应用的标准)来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”(我国著名数学家徐利治).
如图是一个典型的图形模式,用它可测底部可能达不到的建筑物的高度,用它可测河宽,用它可解决数学中的一些问题.等等.
(1)如图,若B1B=30米,∠B1=22°,∠ABC=30°,求AC(精确到1);
(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.40,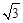 ≈1.73)
≈1.73)
(2)如图,若∠ABC=30°,B1B=AB,计算tan15°的值(保留准确值);
(3)直接写出tan7.5°的值.(注:若出现双重根式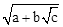 ,则无需化简)
,则无需化简)
(年广东佛山10分)(1)证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;[要求根据图1写出已知、求证、证明;在证明过程中,至少有两处写出推理依据(“已知”除外)
(2)如图2,在▱ABCD中,对角线焦点为O,A1、B1、C1、D1分别是OA、OB、OC、OD的中点,A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点,…,以此类推.
若ABCD的周长为1,直接用算式表示各四边形的周长之和l;
(3)借助图形3反映的规律,猜猜l可能是多少?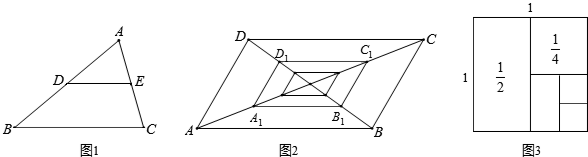
(年浙江温州12分)八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
| 参赛同学 |
答对题数 |
答错题数 |
未答题数 |
| A |
19 |
0 |
1 |
| B |
17 |
2 |
1 |
| C |
15 |
2 |
3 |
| D |
17 |
1 |
2 |
| E |
/ |
/ |
7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知:A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
(年宁夏区10分)某花店计划下个月每天购进80只玫瑰花进行销售,若下个月按30天计算,每售出1只玫瑰花获利润5元,未售出的玫瑰花每只亏损3元.以x(0<x≤80)表示下个月内每天售出的只数,y(单位:元)表示下个月每天销售玫瑰花的利润.根据历史资料,得到同期下个月内市场销售量的频率分布直方图(每个组距包含左边的数,但不包含右边的数)如下图: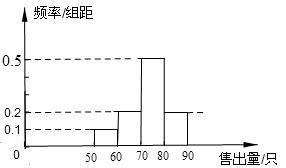
(1)求y关于x的函数关系式;
(2)根据频率分布直方图,计算下个月内销售利润少于320元的天数;
(3)根据历史资料,在70≤x<80这个组内的销售情况如下表:
| 销售量/只 |
70 |
72 |
74 |
75 |
77 |
79 |
| 天数 |
1 |
2 |
3 |
4 |
3 |
2 |
计算该组内平均每天销售玫瑰花的只数.