（本小题满分14分）如图所示，直线
与x轴、y轴分别交于A、B两点，抛物线
经过A、B两点，与x轴的另一个交点为C，连接BC．
（1）求抛物线的解析式及点C的坐标；
（2）点P从点C出发，沿线段CA由C向A运动，同时点Q从点B出发，沿线段BC由B向C运动，P、Q的运动速度都是每秒1个单位长度，当Q点到达C点时，P、Q同时停止运动，试问在坐标平面内是否存在点D，使P、Q运动过程中的某一时刻，以C、D、P、Q为顶点的四边形为菱形？若存在，求出点D的坐标；若不存在，说明理由．
化简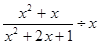
；
化简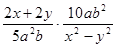
化简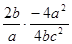
如图1，在正方形ABCD中，等腰三角形AEF的顶点E，F分别在BC和CD上.
（1）求证：BE=DF；
（2）若等腰三角形AEF的腰AE比正方形ABCD的边AB长1，BE=5，求正方形ABCD的面积；
（3）若∠EAF=50°，则
①如图1，∠BAE=°；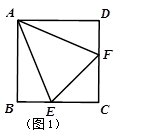
②如图2，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，求∠BAE的大小．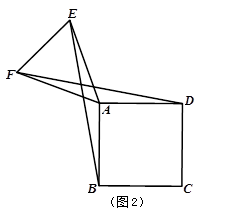
如图，在矩形ABCD中，AC与BD相交于O，∠COD=60°，点E是BC边上的动点，连结DE，OE．
（1）求证：△COD是等边三角形；
（2）如图1，当DE平分∠ADC时，试证明OC=EC，并求出∠DOE的度数；
（3）如图2，当DE平分∠BDC时，试证明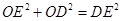
．