如图1,已知抛物线y=ax2+bx (a≠0)经过A(3,0)、B(4,4)两点.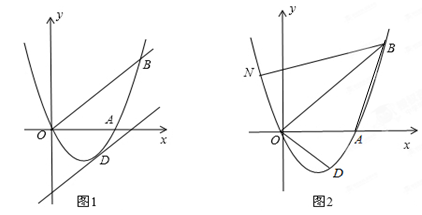
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若异于点A的点N在抛物线上,且∠NBO=∠ABO,求点N的坐标;
(4)在(2)与(3)的条件下,请直接写出所有满足△POD∽△NOB的点P的坐标.
如图,在 中, ,点 是 边的中点,点 在 边上, 经过点 且与 边相切于点 , .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的长.

为了加强学生的体育锻炼,某班计划购买部分绳子和实心球.已知每条绳子的价格比每个实心球的价格少 元,且 元购买绳子的数量与 元购买实心球的数量相同.
(1)绳子和实心球的单价各是多少元?
(2)如果本次购买的总费用为 元,且购买绳子的数量是实心球数量的3倍,那么购买绳子和实心球的数量各是多少?
在贯彻落实“五育并举”的工作中,某校开设了五个社团活动:传统国学(A)、科技兴趣(B)、民族体育(C)、艺术鉴赏(D)、劳技实践(E),每个学生每个学期只参加一个社团活动.为了了解本学期学生参加社团活动的情况,学校随机抽取了若干名学生进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.请根据统计图提供的信息,解答下列问题:

(1)本次调查的学生共有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,传统国学(A)对应扇形的圆心角度数是 ;
(4)若该校有 名学生,请估算本学期参加艺术鉴赏(D)活动的学生人数.
如图,直线 与反比例函数 的图象相交于点 和点 ,与 轴的正半轴相交于点 .
(1)求 的值;
(2)连接 ,若点 为线段 的中点,求 的面积.

综合与实践
“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1,在线段AC同侧有两点 ,连接 ,如果 ,那么 四点在同一个圆上.
探究展示:
如图2,作经过点 的 ,在劣弧 上取一点 (不与 重合),连接 ,则 (依据1)
∵
∴
∴点 四点在同一个圆上(对角互补的四边形四个顶点共圆)
∴点 在点 所确定的 上(依据2)
∴点 四点在同一个圆上
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:__________;依据2:__________.
(2)如图3,在四边形 中, ,则 的度数为_____.
拓展探究:
(3)如图4,已知 是等腰三角形, ,点 在 上(不与 的中点重合),连接 .作点 关于 的对称点 ,连接 并延长交 的延长线于 ,连接 .
①求证: 四点共圆;
②若 , 的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.

