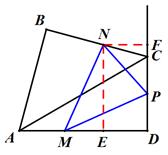
已知，在矩形ABCD中，E为BC边上一点，AE⊥DE，AB=12，BE=16，F为线段BE上一点，EF=7，连接AF．如图①，现有一张硬质纸片△GMN，∠NGM=90°，NG=6，MG=8，斜边MN与边BC在同一直线上，点N与点E重合，点G在线段DE上．如图②，△GMN从图①的位置出发，以每秒1个单位的速度沿EB向点B匀速移动，同时，点P从A点出发，以每秒1个单位的速度沿AD向点D匀速移动，点Q为直线GN与线段AE的交点，连接PQ．当点N到达终点B时，△GMN和点P同时停止运动．设运动时间为t秒，解答下列问题：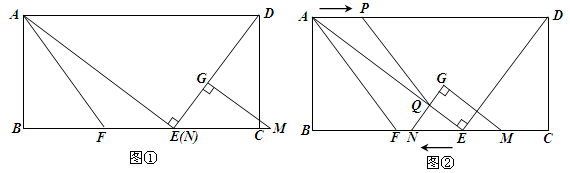
（1）在整个运动过程中，当点G在线段AE上时，求t的值．
（2）在整个运动过程中，是否存在点P，使△APQ是等腰三角形．若存在，求出t的值；若不存在，说明理由．
（3）在整个运动过程中，设△GMN与△AEF重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围．
如图，过原点的直线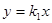
和
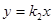与反比例函数
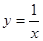的图象分别交于两点A，C和B，D，连结AB，BC，CD，DA．
（1）四边形ABCD一定是 四边形；（直接填写结果）
（2）四边形ABCD可能是矩形吗？若可能，试求此时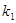
和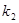
之间的关系式；若不可能，说明理由；
（3）设P（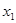
，
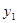），Q（
，
）（
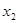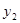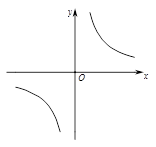
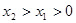）是函数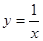图象上的任意两点，
，
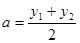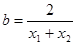，试判断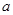
，
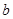的大小关系，并说明理由．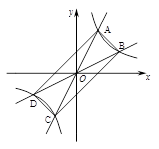
如图1，关于
的二次函数y=－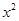
+bx+c经过点A（－3,0），点C（0,3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上。
（1）求抛物线的解析式；
（2）DE上是否存在点P到AD的距离与到轴的距离相等，若存在求出点P，若不存在请说明理由；
（3）如图2，DE的左侧抛物线上是否存在点F，使2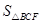
=3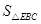
，若存在求出点F的坐标，若不存在请说明理由。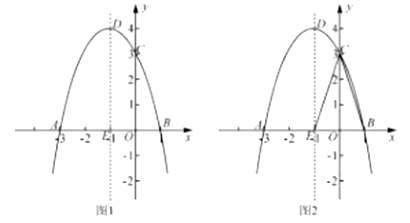
如题25图，在同一平面上，两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起，使斜边AC完全重合，且顶点B，D分别在AC的两旁，∠ABC=∠ADC=90°，∠CAD=30°，AB=BC=4cm．
（1）填空：AD= （cm），DC= （cm）；
（2）点M，N分别从A点，C点同时以每秒1cm的速度等速出发，且分别在AD，CB上沿A→D，C→B的方向运动，当N点运动 到B点时，M，N两点同时停止运动，连结MN，求当M，N点运动了x秒时，点N到AD的距离（用含x的式子表示）；
（3）在（2）的条件下，取DC中点P，连结MP，NP，设△PMN的面积为y（cm2），在整个运动过程中，△PMN的面积y存在最大值，请求出这个最大值．
（参考数据：sin75°=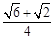
，sin15°=
）
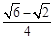如图，在水平地面上竖立着一面墙AB，墙外有一盏路灯D．光线DC恰好通过墙的最高点B，且与地面形成37°角．墙在灯光下的影子为线段AC，并测得AC=5．5米．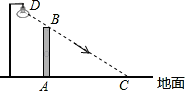
（1）求墙AB的高度（结果精确到0．1米）；（参考数据：tan37°≈0．75，sin37°≈0．60，cos37°≈0．80）
（2）如果要缩短影子AC的长度，同时不能改变墙的高度和位置，请你写出两种不同的方法．
如图，某塔观光层的最外沿点E为蹦极项目的起跳点．已知点E离塔的中轴线AB的距离OE为10米，塔高AB为123米（AB垂直地面BC），在地面C处测得点E的仰角α=45°，从点C沿CB方向前行40米到达D点，在D处测得塔尖A的仰角β=60°，求点E离地面的高度EF．（结果精确到1米，参考数据
≈1．4，
≈1．7）