如图，在水平地面上竖立着一面墙AB，墙外有一盏路灯D．光线DC恰好通过墙的最高点B，且与地面形成37°角．墙在灯光下的影子为线段AC，并测得AC=5．5米．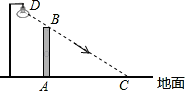
（1）求墙AB的高度（结果精确到0．1米）；（参考数据：tan37°≈0．75，sin37°≈0．60，cos37°≈0．80）
（2）如果要缩短影子AC的长度，同时不能改变墙的高度和位置，请你写出两种不同的方法．
（1）计算：（﹣2）﹣1﹣|﹣
|+（
﹣1）0+cos45°．
（2）已知m2﹣5m﹣14=0，求（m﹣1）（2m﹣1）﹣（m+1）2+1的值．
如图，在平面直角坐标系xoy中，抛物线y=ax2+bx﹣4与x轴交于点A（﹣2，0）和点B，与y轴交于点C，直线x=1是该抛物线的对称轴．
（1）求抛物线的解析式；
（2）若两动点M、H分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行，当点M到达原点时，点H立刻掉头，并以每秒
个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动，经过点M的直线l⊥x轴，交AC或BC于点P，设点M的运动时间为t秒（t＞0）．求点M的运动时间t与△APH的面积S的函数关系式，并求出S的最大值．
在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直线MN过点A且MN∥BC，过点B为一锐角顶点作Rt△BDE，∠BDE=90°，且点D在直线MN上（不与点A重合），如图1，DE与AC交于点P，易证：BD=DP．（无需写证明过程）
（1）在图2中，DE与CA延长线交于点P，BD=DP是否成立？如果成立，请给予证明；如果不成立，请说明理由；
（2）在图3中，DE与AC延长线交于点P，BD与DP是否相等？请直接写出你的结论，无需证明．
某店因为经营不善欠下38400元的无息贷款的债务，想转行经营服装专卖店又缺少资金．“中国梦想秀”栏目组决定借给该店30000元资金，并约定利用经营的利润偿还债务（所有债务均不计利息）．已知该店代理的品牌服装的进价为每件40元，该品牌服装日销售量y（件）与销售价x（元/件）之间的关系可用图中的一条折线（实线）来表示．该店应支付员工的工资为每人每天82元，每天还应支付其它费用为106元（不包含债务）．
（1）求日销售量y（件）与销售价x（元/件）之间的函数关系式；
（2）若该店暂不考虑偿还债务，当某天的销售价为48元/件时，当天正好收支平衡（收人=支出），求该店员工的人数；
（3）若该店只有2名员工，则该店最早需要多少天能还清所有债务，此时每件服装的价格应定为多少元？
如图，矩形OABC的边OA、OC分别在x轴、y轴的正半轴的正半轴上，且OA=3，OC=2，将矩形OABC向上平移4个单位得到矩形O1A1B1C1．
（1）若反比例函数y=
和y=
的图象分别经过点B、B1，求k1和k2的值；
（2）将矩形O1A1B1C1向左平移得到O2A2B2C2，当点O2、B2在反比例函数y=
的图象上时，求平移的距离和k3的值．