如图1,关于 的二次函数y=-
的二次函数y=-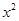 +bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上。
+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上。
(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到 轴的距离相等,若存在求出点P,若不存在请说明理由;
轴的距离相等,若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2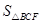 =3
=3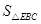 ,若存在求出点F的坐标,若不存在请说明理由。
,若存在求出点F的坐标,若不存在请说明理由。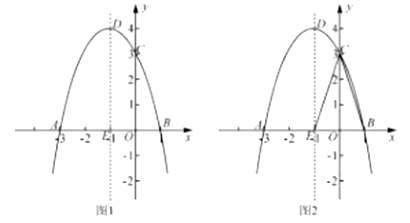
探究:(1)如图①若 .则 .你能说明为什么吗?
(2)反之,若 ,直线 和 有什么位置关系,请证明;
(3)若将点 移至图②所示位置,此时 之间有什么关系?请证明;
(4)若将点 移至图③所示位置,情况又如何?
(5)在图④中, 与 又有何关系?
(6)在图⑤中,若 ,又得到什么结论?

若实数 满足关系式 ,试确定 的值.
如图,将 这 个数字分别填入图中的 个圆圈内,使任意连续相邻的 个圆圈内的数字之和均不大于某一个整数 ,求 的最小值并完成相应的填图游戏.

购买 种数学用品 的件数和用钱总数列成下表:

那么,购买每种数学用品各一件共需多少元?
甲、乙分别自 两地同时相向步行, 后在途中相遇,相遇后,甲、乙步行速度都提高了 ,当甲到达 地后立刻按原路向 地返回.当乙到达 地后也立刻按原路向 地返回.甲、乙二人在第一次相遇后 又再次相遇,则 两地的距离是多少?