(1)某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了 名员工进行调查,所得的数据如下表所示:
名员工进行调查,所得的数据如下表所示:
| |
积极支持改革 |
不太支持改革 |
合 计 |
| 工作积极 |
 |
 |
 |
| 工作一般 |
 |
 |
 |
| 合 计 |
 |
 |
 |
对于人力资源部的研究项目,根据上述数据你能得出什么结论?
(友情提示:当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关; 当
有关; 当 时认为事件
时认为事件 与
与 无关.)
无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
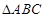 中,
中,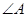 、
、 、
、 所对的边分别为
所对的边分别为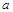 、
、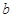 、
、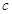
(Ⅰ) 若
若 、
、 、
、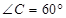 ,求
,求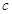 .
. (Ⅱ)若
(Ⅱ)若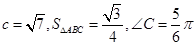 ,
,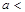
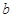 ,求
,求 、
、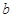 。
。
在△ABC中,a、b、c分别是角A、B、C所对的边,
且acosB十bcosA="1"
(1)求c
(2)若tan(A+B)=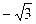 ,求
,求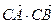 的最大值
的最大值
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Tn.
本题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往相距400 km的灾区.为安全起见,每两辆汽车的前后间距不得小于 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?
已知不等式x2-2x-3<0的解集为A,不等式x2+4x-5<0的解集为B,
(1)求A∪B;
(2)若不等式x2+ax+b<0的解集是A∪B,求ax2+x+b<0的解集