(本小题满分12分) 某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,
, ,
, ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用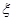 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求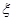 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
AB为圆O的直径,点E、F在圆上,AB//EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1。
(I)求证:BF⊥平面DAF;
(II)求多面体ABCDFE的体积。
已知函数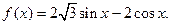
(I)若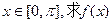 的最大值和最小值;
的最大值和最小值;
(II)若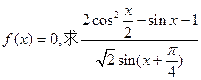 的值。
的值。
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如下表:
| 寿命(h) |
频率 |
| 500600 |
0.10 |
| 600700 |
0.15 |
| 700800 |
0.40 |
| 800900 |
0.20 |
| 9001000 |
0.15 |
| 合计 |
1 |
(I)在下图中补齐频率分布直方图;
(II)估计元件寿命在500800h以内的概率。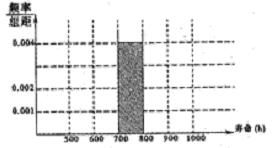
已知数列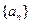 各项均为正数,其前
各项均为正数,其前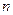 项和
项和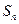 满足
满足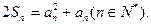
(1)证明: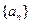 为等差数列
为等差数列
(2)令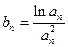 ,记
,记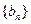 的前
的前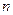 项和为
项和为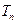 ,求证:
,求证: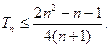
在平面内,设到定点F(0,2)和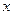 轴距离之和为4的点P轨迹为曲线C,直线
轴距离之和为4的点P轨迹为曲线C,直线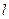 过点F,交曲线C于M,N两点。
过点F,交曲线C于M,N两点。
(1)说明曲线C的形状,并画出图形;
(2)求线段MN长度的范围。