（本小题满分16分）设函数
，
．
（1）当
时，函数
与
在
处的切线互相垂直，求
的值；
（2）若函数
在定义域内不单调，求
的取值范围；
（3）是否存在实数
，使得
对任意正实数
恒成立？若存在，求出满足条件的实数；若不存在，请说明理由．
设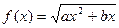
，求满足下列条件的实数
的值：至少有一个正实数
，使函数
的定义域和值域相同。
已知关于
的不等式：
（1）当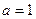
时，求该不等式的解集；（2）当
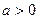时，求该不等式的解集.
已知函数
。
（1）若函数
是
上的增函数，求实数
的取值范围；
（2）当
时，若不等式
在区间
上恒成立，求实数
的取值范围；
（3）对于函数
若存在区间
，使
时，函数的值域也是
，则称是上的闭函数。若函数是某区间上的闭函数，试探求
应满足的条件。
设函数
是定义在
上的偶函数.若当
时，
（1）求在
上的解析式.
（2）请你作出函数的大致图像.
（3）当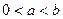
时，若
，求
的取值范围.
（4）若关于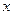
的方程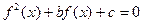
有7个不同实数解，求
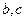满足的条件.
已知函数
.
（1）若
，求
的值；
（2）若
对于
恒成立，求实数
的取值范围.