(本小题满分12分)根据下列算法语句,将输出的A值依次记为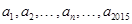

(Ⅰ)求数列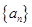 的通项公式;
的通项公式;
(Ⅱ)已知函数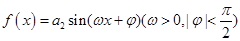 的最小正周期是
的最小正周期是 ,且函数
,且函数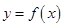 的图象关于直线
的图象关于直线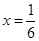 对称,求函数
对称,求函数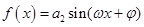 在区间
在区间 上的值域.
上的值域.
已知数列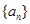 满足
满足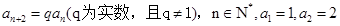 ,且
,且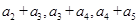 成等差数列.
成等差数列.
(Ⅰ)求q的值和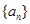 的通项公式;
的通项公式;
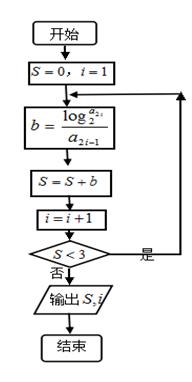
(Ⅱ)若下图所示算法框图中的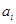 即为(I)中所求,回答以下问题:
即为(I)中所求,回答以下问题:
(1)若记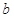 所构成的数列为
所构成的数列为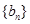 ,求数列
,求数列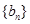 的前
的前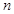 项和
项和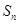
(2)求该框图输出的结果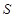 和
和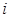
某商场在今年“十一”黄金周期间采取购物抽奖的方式促销(每人至多抽奖一次),设了金奖和银奖,奖券共2000张。在某一时段对30名顾客进行调查,其中有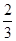 的顾客没有得奖,而得奖的顾客中有
的顾客没有得奖,而得奖的顾客中有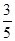 的顾客得银奖,若对这30名顾客随机采访3名顾客。
的顾客得银奖,若对这30名顾客随机采访3名顾客。
(1)求选取的3名顾客中至少有一人得金奖的概率;
(2)求选取的3名顾客中得金奖人数不多于得银奖人数的概率。
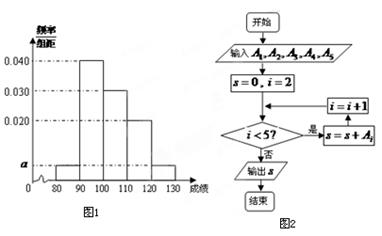
从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图1的频率分布直方图,从左到右各组的频数依次记为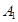 ,
,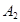 ,
,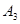 ,
,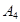 ,
,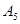 .
.
(1)求图1中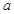 的值;
的值;
(2)图2是统计图1中各组频数的一个算法流程图,求输出的结果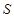 ;
;
(3)从质量指标值分布在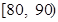 、
、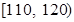 的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.
的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.
已知函数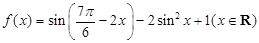 ,
,
(1)求函数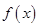 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)在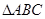 中,三内角
中,三内角 ,
,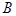 ,
,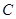 的对边分别为
的对边分别为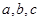 ,已知函数
,已知函数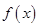 的图象
的图象
经过点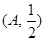 ,
,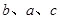 成等差数列,且
成等差数列,且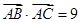 ,求
,求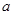 的值.
的值.
设函数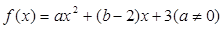 ,
,
(1)若不等式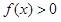 的解集
的解集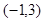 ,求
,求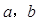 的值;
的值;
(2)若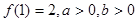 ,求
,求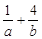 的最小值.
的最小值.