(本小题满分10分)选修4-4:坐标系与参数方程
将圆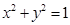 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线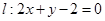 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与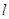 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
对于x∈R,不等式|x-1|+|x-2|≥ 2+
2+ 2恒成立,试求2
2恒成立,试求2 +
+ 的最大值。
的最大值。
已知曲线C1: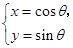 (
(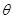 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线 .写出
.写出 的参数方程.
的参数方程. 与
与 公共点的个数和C
公共点的个数和C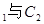 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
(1)设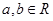 ,若矩阵A=
,若矩阵A= 的变换把直线
的变换把直线 变换为另一直线
变换为另一直线 .
.
(1)求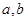 的值;
的值;
(2)求矩阵A的特征值.
设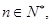 圆
圆 与
与 轴正半轴的交点为
轴正半轴的交点为 ,与曲线
,与曲线 的交点为
的交点为 ,直线
,直线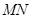 与
与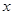 轴的交点为
轴的交点为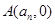 .
.
(1)用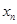 表示
表示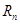 和
和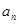
(2)若数列 满足
满足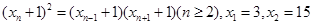
(1)求常数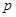 的值,使得数列
的值,使得数列 成等比数列;
成等比数列;
(2)比较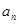 与
与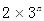 的大小.
的大小.
设椭圆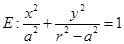 的焦点在
的焦点在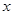 轴上,
轴上, 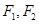 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点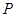 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线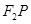 交
交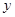 轴于点
轴于点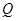 ,
,
(1)当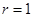 时,
时,
(1)若椭圆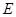 的离心率为
的离心率为 ,求椭圆
,求椭圆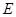 的方程;
的方程;
(2)当点P在直线 上时,求直线
上时,求直线 与
与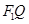 的夹角;
的夹角;
(2) 当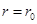 时,若总有
时,若总有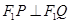 ,猜想:当
,猜想:当 变化时,点
变化时,点 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).