已知曲线C1: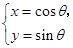 (
(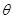 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线 .写出
.写出 的参数方程.
的参数方程. 与
与 公共点的个数和C
公共点的个数和C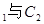 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
设抛物线 的焦点为
的焦点为 ,经过点
,经过点 的动直线
的动直线 交抛物线
交抛物线 于点
于点 ,
, 且
且 .
.
(1)求抛物线 的方程;
的方程;
(2)若 (
( 为坐标原点),且点
为坐标原点),且点 在抛物线
在抛物线 上,求直线
上,求直线 倾斜角;
倾斜角;
(3)若点 是抛物线
是抛物线 的准线上的一点,直线
的准线上的一点,直线 的斜率分别为
的斜率分别为 .求证:
.求证:
当 为定值时,
为定值时, 也为定值.
也为定值.
某医药研究所开发一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量 (微克)与时间
(微克)与时间 (小时)之间满足
(小时)之间满足 ,
,
其对应曲线(如图所示)过点 .
.
(1)试求药量峰值( 的最大值)与达峰时间(
的最大值)与达峰时间( 取最大值时对应的
取最大值时对应的 值);
值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
已知复数 (
( 为虚数单位)
为虚数单位)
(1)若 ,且
,且 ,求
,求 与
与 的值;
的值;
(2)设复数 在复平面上对应的向量分别为
在复平面上对应的向量分别为 ,若
,若 ,且
,且 ,求
,求 的最小正周期和单调递减区间.
的最小正周期和单调递减区间.
已知正四棱柱 的底面边长为2,
的底面边长为2, .
.
(1)求该四棱柱的侧面积与体积;
(2)若 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的大小.
所成角的大小.
已知函数 ,
, (其中
(其中 ,
, ),且函数
),且函数 的图象在点
的图象在点 处的切线与函数
处的切线与函数 的图象在点
的图象在点 处的切线重合.
处的切线重合.
(Ⅰ)求实数a,b的值;
(Ⅱ)若 ,满足
,满足 ,求实数m的取值范围;
,求实数m的取值范围;