已知函数 .
.
(1)求函数 的零点,并求反函数
的零点,并求反函数 ;
;
(2)设 ,若不等式
,若不等式 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的范围.
的范围.
(本题满分14分) 本题有2个小题,第一小题满分6分,第二小题满分8分。
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.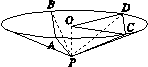
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
给定函数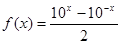
(1)求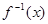 ;
;
(2)判断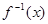 的奇偶性,并证明你的结论。
的奇偶性,并证明你的结论。
(本小题满分12分)设函数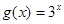 ,
,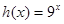 .
.
(1)解方程: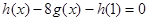 ;
;
(2)令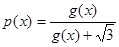 ,求证:
,求证: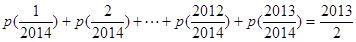 ;
;
(3)若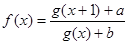 是实数集
是实数集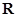 上的奇函数,且
上的奇函数,且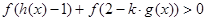 对任意实数
对任意实数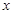 恒成立,求实数
恒成立,求实数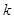 的取值范围.
的取值范围.
(参考公式:当a>0,b>0时,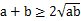 ,当且仅当a=b时等号成立)
,当且仅当a=b时等号成立)
(本小题满分10分)已知函数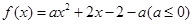 ,
,
(1)若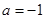 ,求函数的零点;
,求函数的零点;
(2)若函数在区间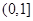 上恰有一个零点,求
上恰有一个零点,求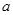 的取值范围.
的取值范围.
(本小题满分10分)已知函数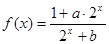 是奇函数,并且函数
是奇函数,并且函数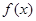 的图像经过点
的图像经过点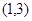 .
.
(1)求实数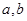 的值;
的值;
(2)求函数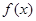 在
在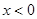 时的值域.
时的值域.