(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西36.9°方向,求此时轮船所处位置B与城市P的距离?(参考数据:sin36.9°≈ ,tan36.9°≈
,tan36.9°≈ ,sin67.5°≈
,sin67.5°≈ ,tan67.5°≈
,tan67.5°≈ )
)
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.
求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,
(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.
某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到
一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计(图
中信息不完整). 已知A、B两组捐款人数的比为1 : 5.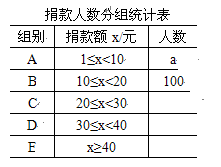
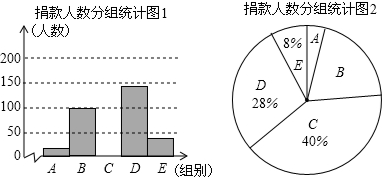
请结合以上信息解答下列问题.
(1) a=,本次调查样本的容量是;
(2) 先求出C组的人数,再补全“捐款人数分组统计图1”;
(3) 若任意抽出1名学生进行调查,恰好是捐款数不少于30元的概率是多少?