如图1,是边长分别为6和4的两个等边三角形纸片ABC和CD1E1叠放在一起.
(1)操作:固定△ABC,将△CD1E1绕点C顺时针旋转得到△CDE,连接AD、BE,如图2.探究:在图2中,线段BE与AD之间有怎样的大小关系?并请说明理由;
(2)操作:固定△ABC,若将△CD1E1绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于点F,在线段CF上沿着CF方向平移,(点F与点P重合即停止平移)平移后的△CDE设为△PQR,如图3.
探究:在图3中,除三角形ABC和CDE外,还有哪个三角形是等腰三角形?写出你的结论(不必说明理由);
(3)探究:如图3,在(2)的条件下,设CQ=x,用x代数式表示出GH的长.
在一个不透明的袋中装有2个黄球,3个黑球和5个红球,它们除颜色外其他都相同.
(1)将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;
(2)现在再将若干个红球放入袋中,与原来的10个球均匀混合在一起,使从袋中随机摸出一个球是红球的概率是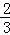 ,请求出后来放入袋中的红球的个数.
,请求出后来放入袋中的红球的个数.
某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图: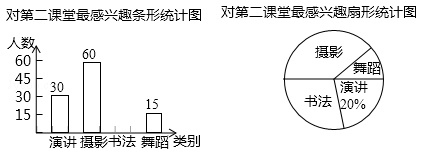
(1)此次调查抽取的学生人数m=名,其中选择"书法"的学生占抽样人数的百分比n=;
(2)若该校有3000名学生,请根据以上数据估计该校对"书法"最感兴趣的学生人数.
补充完整三角形中位线定理,并加以证明:
(1)三角形中位线定理:三角形的中位线;
(2)已知:如图,DE是△ABC的中位线,求证:DE∥BC,DE=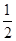 BC.
BC.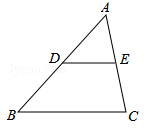
设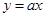 ,若代数式
,若代数式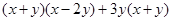 化简的结果为
化简的结果为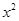 ,请你求出满足条件的a值.
,请你求出满足条件的a值.
已知,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点C.

(1)求此抛物线的解析式;
(2)如图1,点E是线段OB上一动点,过点E作DE⊥x轴,交抛物线于点D,若直线CD与以OE为直径的⊙M相切,试求出点E的坐标;
(3)如图2,在抛物线上是否存在一点P,过点P作x轴的垂线,垂足为F,过点F作FG∥BC,交线段AC于点G,连接FC,使△BCF∽△CFG?若存在,求出点P的坐标;若不存在,请说明理由.