【2015高考福建,文18】全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
| 组号 |
分组 |
频数 |
| 1 |
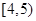 |
2 |
| 2 |
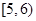 |
8 |
| 3 |
 |
7 |
| 4 |
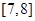 |
3 |
(Ⅰ)现从融合指数在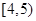 和
和 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
已知矩阵A=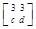 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1= ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2=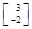 .求矩阵A,并写出A的逆矩阵.
.求矩阵A,并写出A的逆矩阵.
(本小题满分16分)
已知 ,
,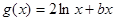 ,且直线
,且直线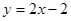 与曲线
与曲线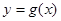 相切.
相切.
(1)若对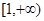 内的一切实数
内的一切实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,求最大的正整数
时,求最大的正整数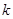 ,使得对
,使得对 (
( 是自然对数的底数)内的任意
是自然对数的底数)内的任意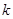 个实数
个实数 都有
都有 成立;
成立;
(3)求证:
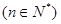 .
.
已知有穷数列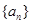 共有
共有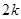 项(整数
项(整数 ),首项
),首项 ,设该数列的前
,设该数列的前 项和为
项和为 ,且
,且 其中常数
其中常数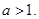 ⑴求
⑴求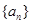 的通项公式;⑵若
的通项公式;⑵若 ,数列
,数列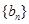 满足
满足
求证: ;
;
⑶若⑵中数列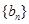 满足不等式:
满足不等式: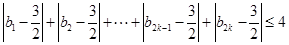 ,求
,求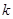 的最大值.
的最大值.
(本小题满分15分)
给定椭圆C: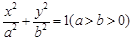 ,称圆心在原点O、半径是
,称圆心在原点O、半径是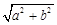 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为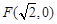 ,其短轴的一个端点到点
,其短轴的一个端点到点 的距离为
的距离为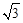 .
.
(1)求椭圆C和其“准圆”的方程;
(2)若点 是椭圆C的“准圆”与
是椭圆C的“准圆”与 轴正半轴的交点,
轴正半轴的交点,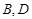 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且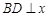 轴,求
轴,求 的取值范围;
的取值范围;
(3)在椭圆C的“准圆”上任取一点 ,过点
,过点 作直线
作直线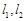 ,使得
,使得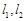 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断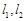 是否垂直?并说明理由.
是否垂直?并说明理由.
(本小题满分15分)
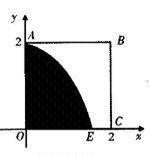
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数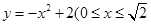 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为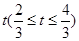 .
.
(1)当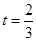 时,求直路
时,求直路 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?