【2015高考福建,理19】已知函数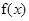 的图像是由函数
的图像是由函数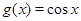 的图像经如下变换得到:先将
的图像经如下变换得到:先将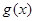 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移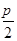 个单位长度.
个单位长度.
(Ⅰ)求函数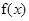 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于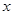 的方程
的方程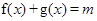 在
在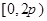 内有两个不同的解
内有两个不同的解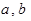 .
.
(1)求实数m的取值范围;
(2)证明: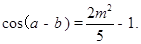
近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽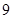 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,
请计算出统计量 ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
下面的临界值表供参考:
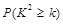 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式 ,其中
,其中 )
)
| 患三高疾病 |
不患三高疾病 |
合计 |
|
| 男 |
6 |
30 |
|
| 女 |
|||
| 合计 |
36 |
如图五面体中,四边形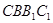 为矩形,
为矩形, ,四边形
,四边形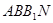 为梯形,
为梯形,
且 ,
,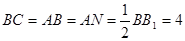 .
.
(1)求证: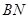
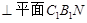 ;
;
(2)求此五面体的体积.
在公差不为零的等差数列{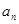 }中,
}中,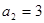 ,
,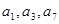 成等比数列.
成等比数列.
(1)求数列{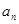 }的通项公式;
}的通项公式;
(2)设数列{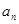 }的前
}的前 项和为
项和为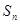 ,记
,记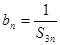 .求数列
.求数列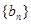 的前
的前 项和
项和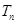 .
.
不等式选讲
已知正实数 满足:
满足: .
.
(1)求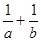 的最小值
的最小值 ;
;
(2)设函数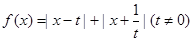 ,对于(1)中求得的
,对于(1)中求得的 ,是否存在实数
,是否存在实数 ,使得
,使得 成立,说明理由.
成立,说明理由.
已知直线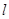 :
: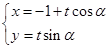 (
(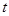 为参数,a为
为参数,a为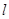 的倾斜角),以坐标原点为极点,
的倾斜角),以坐标原点为极点,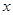 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 为:
为: .
.
(1)若直线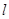 与曲线
与曲线 相切,求
相切,求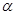 的值;
的值;
(2)设曲线 上任意一点的直角坐标为
上任意一点的直角坐标为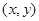 ,求
,求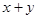 的取值范围.
的取值范围.