【2015高考安徽,理18】设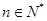 ,
,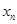 是曲线
是曲线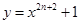 在点
在点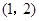 处的切线与x轴交点的横坐标.
处的切线与x轴交点的横坐标.
(Ⅰ)求数列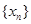 的通项公式;
的通项公式;
(Ⅱ)记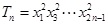 ,证明
,证明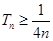 .
.
已知在△ABC中,角A,B,C的对边分别是a,b,c,满足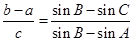 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
(1)求角A的值;
(2)求f(C)=2sinC·cosB的值域.
已知函数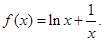
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)若g(x)=f(x)一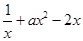 有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
(3)设q>p>2,求证:当x∈(p,q)时,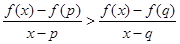 .
.
在平面直角坐标系xoy中,以点P为圆心的圆与圆x2+y2-2y=0外切且与x轴相切(两切点不重合).
(1)求动点P的轨迹方程;
(2)若直线mx一y+2m+5=0(m∈R)与点P的轨迹交于A、B两点,问:当m变化时,以线段AB为直径的圆是否会经过定点?若会,求出此定点;若不会,说明理由.
设数列{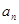 }满足:a1=2,对一切正整数n,都有
}满足:a1=2,对一切正整数n,都有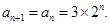
(1)探讨数列{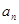 }是否为等比数列,并说明理由;
}是否为等比数列,并说明理由;
(2)设
四棱锥P—ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱 ,
,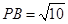 ,M、N两点分别在侧棱PB、PD上,
,M、N两点分别在侧棱PB、PD上,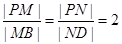 .
.
(1)求证:PA⊥平面MNC。
(2)求平面NPC与平面MNC的夹角的余弦值.