【2015高考北京，理16】
，
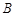两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下：
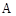组：10，11，12，13，14，15，16
组：12，13，15，16，17，14，
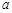
假设所有病人的康复时间互相独立，从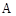，两组随机各选1人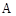，组选出的人记为甲，组选出的人记为乙．
（Ⅰ）求甲的康复时间不少于14天的概率；
（Ⅱ）如果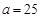
，求甲的康复时间比乙的康复时间长的概率；
（Ⅲ）当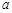为何值时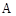，，两组病人康复时间的方差相等？（结论不要求证明）
已知函数
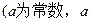＞0）
（1）若
的一个极值点，求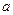
的值；
（2）求证：当0＜
上是增函数；
（3）若对任意的
总存在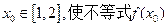
＞
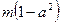成立，求实数m的取值范围。
我校高二年级
举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰，已知选手甲答题连续两次答错的概率为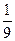
（已知甲回答每个问题的正确率相同，并且相互之间没有影响）.
（1）求甲选手回答一个问题的正确率；
（2）求选手甲可进入决赛的概率；
（3）设选手甲在初赛中答题的个数为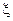
，试写出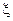的分布列，并求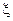的数学期望.
在极坐标系中，极点为坐标原点O，已知圆C的圆心坐标为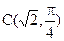
，半径
为
，直线
的极坐标方程为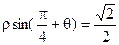
.
（1）求圆C的极坐标方程；
（2）若圆C和直线相交于A，B两点，求线段AB的长.
已知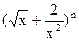
的第五项的二项式系数与第三项的二项式系数比为14:3,求展开式中的常数项.