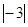(本题4分)若(x﹣1)(x2+mx+n)=x3﹣6x2+11x﹣6,求m,n的值.
(本大题15分)画线段MN=3㎝,在线段MN上取一点Q,使MQ=NQ,延长线段MN至点A,使AN=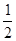 MN;延长线段NM至点B
MN;延长线段NM至点B ,使BN=3BM,根据所画图形计算:
,使BN=3BM,根据所画图形计算: 线段BM的长度;
线段AN的长度;
试说明Q是哪些线段的中点?图中
 共有多少条线段
共有多少条线段 ?它们分别是?
?它们分别是?
(本大题8分)已知关于x的方程 =x+
=x+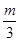 与
与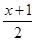 =3x-2的解互为倒数,求m的值?
=3x-2的解互为倒数,求m的值?
(本大题12分(1)5分、(2)7分)(1).已知x<-4,化简│-x│+│x+4│-│x-4│
(2)把一批图书分给某班
 学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本。问有多少本图书?多少名学生?
学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本。问有多少本图书?多少名学生?
(本大题共计14分)(1)计算-(
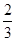 )2×9-2×(-
)2×9-2×(-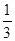 )÷
)÷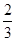 +4×(-0.5)2
+4×(-0.5)2(2)解方程:
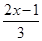 -
- =
=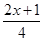 -1
-1
(1)先化简,再求值2(m2n+mn2)-2(m2n-1)-3(mn2+1),
其中m=-2,n=2(2)将下列各数在数轴上表示
 出来,并用“<”连接:
出来,并用“<”连接:
-22, -(-1), 0,-│-2│ , -2.5,
, -2.5,