【2015高考湖南,理21】已知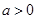 ,函数
,函数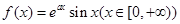 ,记
,记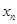 为
为 的从小到大的第
的从小到大的第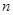
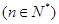 个极值点,证明:
个极值点,证明:
(1)数列 是等比数列
是等比数列
(2)若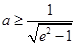 ,则对一切
,则对一切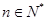 ,
,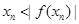 恒成立.
恒成立.
已知椭圆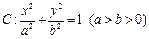 的离心率为
的离心率为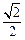 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线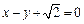 相切.
相切.
(Ⅰ)求椭圆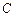 的方程;
的方程;
(Ⅱ)若过点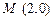 的直线与椭圆
的直线与椭圆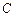 相交于两点
相交于两点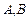 ,设
,设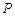 为椭圆上一点,且满足
为椭圆上一点,且满足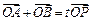 (
(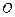 为坐标原点),当
为坐标原点),当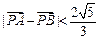 时,求实数
时,求实数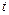 的取值范围
的取值范围
已知函数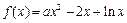 .
.
(Ⅰ)若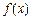 无极值点,但其导函数
无极值点,但其导函数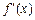 有零点,求
有零点,求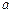 的值;
的值; (Ⅱ)若
(Ⅱ)若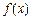 有两个极值点,求
有两个极值点,求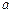 的取值范围,并证明
的取值范围,并证明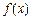 的极小值小于
的极小值小于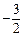
已知等差数列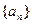 的前
的前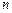 项和为
项和为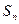 ,且
,且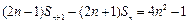
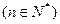 .
.
(Ⅰ)求数列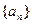 的通项公式;
的通项公式;
(Ⅱ)求证: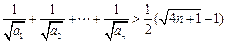
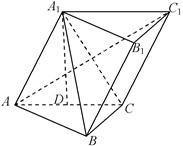
己知三棱柱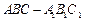 ,
,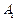 在底面ABC上的射影恰为AC的中点D,
在底面ABC上的射影恰为AC的中点D,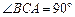 ,
,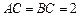 ,又知
,又知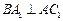
(Ⅰ)求证: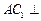 平面
平面
 ;
;
(Ⅱ)求点C到平面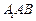 的距离;
的距离;
(Ⅲ)求二面角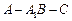 余弦值的大小.
余弦值的大小.
小白鼠被注射某种药物后,只会表现为以下三种症状中的一种:兴奋、无变化(药物没有发生作用)、迟钝.若出现三种症状的概率依次为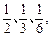 现对三只小白鼠注射
现对三只小白鼠注射 这种药物.
这种药物.
(Ⅰ)求这三只小白鼠表现症状互不相同的概率;
(Ⅱ)用 表示三只小白鼠共表现症状的种数,求
表示三只小白鼠共表现症状的种数,求 的分布列及数学期望
的分布列及数学期望