【2015高考天津,理17】(本小题满分13分)如图,在四棱柱 中,侧棱
中,侧棱 ,
, ,
, ,
,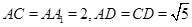 ,且点M和N分别为
,且点M和N分别为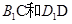 的中点.
的中点.
(Ⅰ)求证: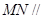 平面
平面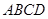 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)设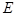 为棱
为棱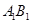 上的点,若直线
上的点,若直线 和平面
和平面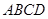 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段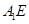 的长
的长
数列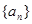 ,满足
,满足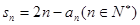
(1)求 ,并猜想通项公式
,并猜想通项公式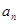 。
。
(2)用数学归纳法证明(1)中的猜想。
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程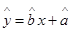 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注: )
)
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为 和
和 ,求(1)恰有1人译出密码的概率;
,求(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为 ,至少需要多少个乙这样的人?
,至少需要多少个乙这样的人?
从4名男生,3名女生中选出三名代表。
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都要有的不同的选法共有多少种?
在△ABC中,内角A、B、C所对边的边长分别是a、b、c,已知c=2,C=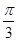 .
.
(Ⅰ)若△ABC的面积等于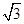 ,求a、b;
,求a、b;
(Ⅱ)若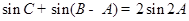 ,求△ABC的面积.
,求△ABC的面积.