【2015高考湖北,理19】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马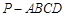 中,侧棱
中,侧棱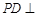 底面
底面 ,且
,且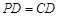 ,过棱
,过棱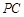 的中点
的中点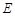 ,作
,作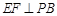 交
交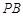 于点
于点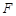 ,连接
,连接
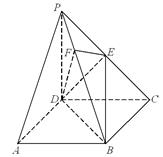
(Ⅰ)证明: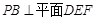 .试判断四面体
.试判断四面体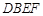 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面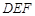 与面
与面 所成二面角的大小为
所成二面角的大小为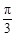 ,求
,求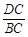 的值.
的值.
某种食品是经过 、
、 、
、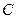 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、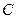 工序的产品合格率分别为
工序的产品合格率分别为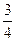 、
、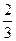 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
(Ⅰ)正式生产前先试生产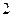 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率;
(Ⅱ)设 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求 的分布列和数学期望.
的分布列和数学期望.
已知两点 ,点
,点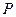 为坐标平面内的动点,且满足
为坐标平面内的动点,且满足 .
.
(Ⅰ)求点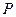 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线 斜率为
斜率为 ,且与曲线
,且与曲线 相交于点
相交于点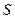 、
、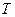 ,若
,若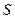 、
、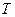 两点只在第二象限内运动,线段
两点只在第二象限内运动,线段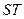 的垂直平分线交
的垂直平分线交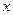 轴于
轴于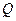 点,求
点,求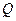 点横坐标的取值范围.
点横坐标的取值范围.
已知函数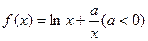 ,直线
,直线 与函数
与函数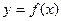 图象相切.
图象相切.
(Ⅰ)求直线 的斜率
的斜率 的取值范围;
的取值范围;
(Ⅱ)设函数 ,已知函数
,已知函数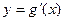 的图象经过点
的图象经过点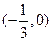 ,求函数
,求函数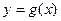 的极值.
的极值.
在数列 中,
中,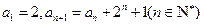 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)设数列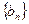 满足
满足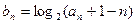 ,若
,若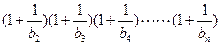
 对一切
对一切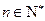 且
且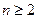 恒成立,求实数
恒成立,求实数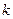 的取值范围.
的取值范围.
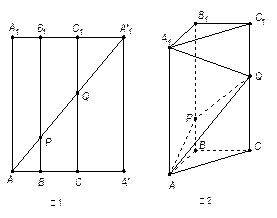 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形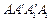 中,
中,
 ,且
,且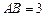 ,
,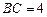 ,
, 分别交
分别交
 于点
于点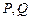 ,将该正方形沿
,将该正方形沿 、
、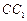 折叠,使得
折叠,使得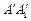 与
与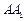 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱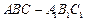 中
中
(Ⅰ)求证:
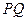 ;
;
(Ⅱ)在底边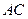 上有一点
上有一点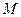 ,
,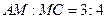 ,
,
求证: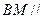 面
面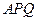
(III)求直线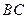 与平面
与平面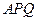 所成角的正弦值.
所成角的正弦值.