C(选修4—4:坐标系与参数方程)
已知圆C的极坐标方程为 ,求圆C的半径.
,求圆C的半径.
(本题满分12分)
若不等式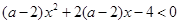 对一切
对一切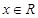 恒成立, 求
恒成立, 求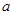 的取值范围。
的取值范围。
本题满分10分)
一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是 海里,则灯塔和轮船原来的距离为多少?
海里,则灯塔和轮船原来的距离为多少?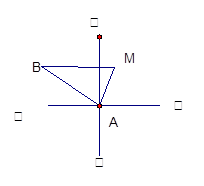
已知圆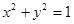 过椭圆
过椭圆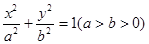 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个 与圆
与圆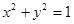 相切 ,与椭圆
相切 ,与椭圆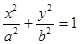 相交于
相交于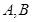 两点记
两点记
(1)求椭圆的方程
(2)求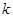 的取值范围;
的取值范围;
(3)求 的面积S的取值范围.
的面积S的取值范围.
已知过点 的动直线
的动直线 与抛物线
与抛物线 相交于
相交于 两点,当直线
两点,当直线 的斜率是
的斜率是 时,
时, 。
。
(1)求抛物线 的方程;(5分)
的方程;(5分)
(2)设线段 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为 ,求
,求 的取值范围。(7分)
的取值范围。(7分)
已知椭圆 中心在原点,一个焦点为
中心在原点,一个焦点为 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是 。
。
(1)求椭圆 的方程;(5分)
的方程;(5分)
(2)是否存在斜率为 的直线
的直线 ,使直线
,使直线 与椭圆
与椭圆 有公共点,且原点
有公共点,且原点 与直线
与直线 的距离等于4;若存在,求出直线
的距离等于4;若存在,求出直线 的方程,若不存在,说明理由。(7分)。
的方程,若不存在,说明理由。(7分)。