(本小题满分10分)已知数列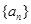 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中 ,且
,且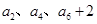 成等比数列;数列
成等比数列;数列 的前
的前 项和为
项和为 ,满足
,满足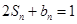 .
.
(1)求数列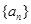 、
、 的通项公式;
的通项公式;
(2)如果 ,设数列
,设数列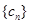 的前
的前 项和为
项和为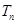 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立,若存在,求出
成立,若存在,求出 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
如图,在四面体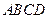 中,
中,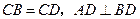 ,点
,点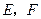 分别是
分别是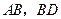 的中点.
的中点.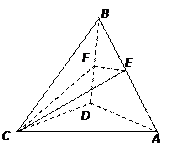
求证:(1)直线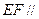 面
面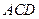 ;
;
(2)平面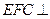 面
面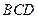 .
.
已知函数f(x)=

(1)、求f(2)与f( ),f(3)与f(
),f(3)与f( );
);
(2)、由(1)中求得结果,你能发现f(x) 与f(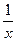 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;
(3)、求f(1)+f(2)+f(3)+ 的值.
的值.
已知直线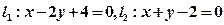 ,设其交点为点P。
,设其交点为点P。
(1)求交点P的坐标;
(2)设直线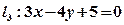 ,分别求过点P且与直线
,分别求过点P且与直线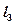 平行和垂直的直线方程.
平行和垂直的直线方程.
已知集合M={x|x2-3x+2=0},N={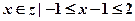 },Q={1,a2+1,a+1}
},Q={1,a2+1,a+1}
(1).求:M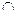 N;(2) .若M
N;(2) .若M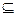 Q,求实数a的值。
Q,求实数a的值。
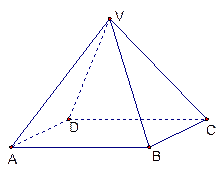 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为 的等腰三角形,求二面角V-AB-C的大小.
的等腰三角形,求二面角V-AB-C的大小.