某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.

根据以上信息解答下列问题:
(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角的度数为 ;
(2)把条形统计图补充完整;
(3)若将:“稍加询问”和“从来不管”视为“管理不严”,已知学校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
甲乙两公司生产同一种新产品,经测算,对于函数 ,
, ,及任意的
,及任意的 ,当甲公司投入
,当甲公司投入 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入 万元作宣传时,甲公司投入的宣传费若小于
万元作宣传时,甲公司投入的宣传费若小于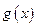 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
(1)请解释 ;
;
(2)甲、乙两公司在均无失败危险的情况下尽可能少地投入宣传费用,问此时各应投入多少宣传费?
(3)若甲、乙分别在上述策略下,为确保无失败的危险,根据对方所投入的宣传费,按最少投入费用原则,投入自己的宣传费:若甲先投入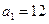 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用 ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为 ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为
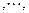 如此得当甲调整宣传费为
如此得当甲调整宣传费为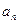 时,乙调整宣传费为
时,乙调整宣传费为 ;试问是否存在
;试问是否存在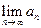 ,
, 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由.
已知函数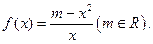
(1)设 ,当m≥
,当m≥ 时,求g(x)在[
时,求g(x)在[ ]上的最大值;
]上的最大值;
(2)若 上是单调减函数,求实数m的取值范围.
上是单调减函数,求实数m的取值范围.
已知 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))
(I) 若 ,求函数
,求函数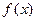 的单调递增区间;
的单调递增区间;
(II)若函数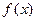 的导函数
的导函数 满足:当|x|≤1时,有|
满足:当|x|≤1时,有| |≤
|≤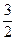 恒成立,求函数
恒成立,求函数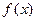 的解析表达式;
的解析表达式;
(III)若0<a<b, 函数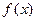 在
在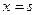 和
和 处取得极值,且
处取得极值,且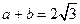 ,证明:
,证明: 与
与 不可能垂直.
不可能垂直.
已知二次函数 为常数);
为常数); .若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
.若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
(Ⅰ)求a、b、c的值;
(Ⅱ)求阴影面积S关于t的函数S(t)的解析式;
(Ⅲ)若 问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
已知函数 ,函数
,函数 .
.
(1)当 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)设函数h(x)=(1-x)f(x)+16,试根据m的取值分析函数h(x)的图象与函数g(x)的图象交点的个数.