(本小题共13分)已知函数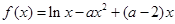 .
.
(Ⅰ)若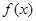 在
在 处取得极值,求a的值;
处取得极值,求a的值;
(Ⅱ)求函数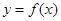 在
在 上的最大值.
上的最大值.
(本小题共13分)已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△ ,使得平面
,使得平面 ⊥平面ABD.
⊥平面ABD.
(Ⅰ)求证: 平面ABD;
平面ABD;
(Ⅱ)求直线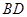 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题共14分)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
(本小题共13分)已知等差数列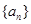 的前
的前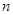 项和为
项和为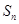 ,a2=4, S5=35.
,a2=4, S5=35.
(Ⅰ)求数列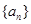 的前
的前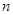 项和
项和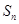 ;
;
(Ⅱ)若数列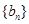 满足
满足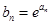 ,求数列
,求数列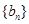 的前n项和
的前n项和 .
.
(本小题满分10分)选修4-5:不等式选讲.
已知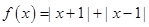 ,不等式
,不等式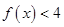 的解集为M.
的解集为M.
(1)求M;
(2)当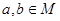 时,证明:
时,证明: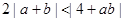 .
.