如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米,设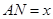 米,花坛AMPN的面积为
米,花坛AMPN的面积为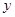 平方米
平方米
(1)求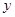 关于
关于 的函数解析式和定义域;
的函数解析式和定义域;
(2)要使花坛AMPN的面积大于32平方米,求 的取值范围;
的取值范围;
(3)当AM,AN的长度分别是多少时,花坛AMPN的面积最小,并求出最小面积.
已知数列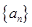 的首项
的首项 的等比数列,其前
的等比数列,其前 项和
项和 中
中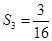 ,
,
(1)求数列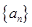 的通项公式;
的通项公式;
(2)设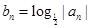 ,
, ,求证:
,求证:
已知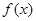
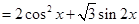
(Ⅰ)求函数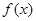 的单调递增区间;
的单调递增区间;
(Ⅱ)在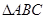 中,
中,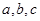 分别是角A,B,C的对边,
分别是角A,B,C的对边,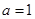 且
且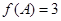 ,求
,求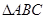 的面积
的面积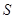 的最大值.
的最大值.
已知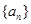 是公比大于1的等比数列,
是公比大于1的等比数列,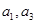 是函数
是函数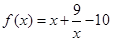 的两个零点。
的两个零点。
(1)求数列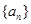 的通项公式;
的通项公式;
(2)若数列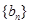 满足
满足 ,且
,且 ,求
,求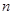 的最小值。
的最小值。
(本小题满分14分)(注意:在试题卷上作答无效)
已知曲线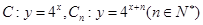 ,从
,从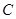 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交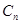 于点
于点 ,再从点
,再从点 作
作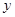 轴的垂线,交
轴的垂线,交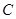 于点
于点 ,设
,设
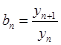
(1)求数列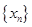 的通项公式;
的通项公式;
(2)记 ,数列
,数列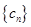 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小
的大小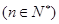 ;
;
(3)记 ,数列
,数列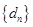 的前
的前 项和为
项和为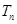 ,试证明:
,试证明:

(本小题14分,计入总分)
已知数列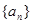 满足:
满足: 
⑴求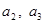 ;
;
⑵当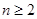 时,求
时,求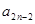 与
与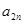 的关系式,并求数列
的关系式,并求数列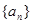 中偶数项的通项公式;
中偶数项的通项公式;
⑶求数列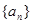 前100项中所有奇数项的和.
前100项中所有奇数项的和.