(本小题满分12分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若 ,求实数m的取值范围.
,求实数m的取值范围.
已知f(x)是偶函数而且在(0,+∞)上是减函数,判断f(x)在(-∞,0)上的增减性并加以证明.
在Rt△ABC中,∠C=90°,以斜边AB所在直线为轴将△ABC旋转一周生成两个圆锥,设这两个圆锥的侧面积之积为S1,△ABC的内切圆面积为S2,记 =x.
=x.
(1)求函数f(x)=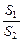 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域.
(2)求函数f(x)的最小值.
某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台.已知生产家电产品每台所需工时和每台产值如下表:
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工时 |
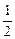 |
 |
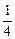 |
| 产值(千元) |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
已知函数f(x)=lg[(a2-1)x2+(a+1)x+1]
(1)若f(x)的定义域为(-∞,+∞),求实数a的取值范围;
(2)若f(x)的值域为(-∞,+∞),求实数a的取值范围
某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-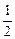 x2(万元)(0≤x≤5),其中x是产品售出的数量(单位: 百台)
x2(万元)(0≤x≤5),其中x是产品售出的数量(单位: 百台)
(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?