(本小题满分13分)已知函数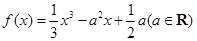 .
.
(Ⅰ)若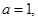 求函数
求函数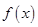 在
在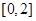 上的最大值;
上的最大值;
(Ⅱ)若对任意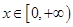 ,有
,有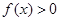 恒成立,求
恒成立,求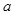 的取值范围.
的取值范围.
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min。
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间 的分布列及期望。
如图,在三棱锥 中, 底面 ,点 , 分别在棱 上,且

(Ⅰ)求证: 平面 ;
(Ⅱ)当 为 的中点时,求 与平面 所成的角的大小;
(Ⅲ)是否存在点 使得二面角 为直二面角?并说明理由。
在 中,角 的对边分别为 , 。
(Ⅰ)求 的值;
(Ⅱ)求 的面积。
设各项均为正数的数列 满足 .
(Ⅰ)若 求 , ,并猜想 的值(不需证明);
(Ⅱ)若 对 恒成立,求 的值.
如图, 和 是平面上的两点,动点 满足:

(Ⅰ)求点 的轨迹方程;
(Ⅱ)设 为点 到直线 : 的距离,若 ,求 的值.