(本小题满分12分)设函数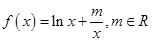 .
.
(Ⅰ)当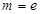 (
(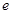 为自然对数的底数)时,求
为自然对数的底数)时,求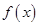 的极小值;
的极小值;
(Ⅱ)讨论函数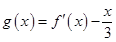 零点的个数;
零点的个数;
(Ⅲ)若对任意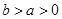 ,
,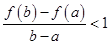 恒成立,求
恒成立,求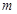 取值范围.
取值范围.
(本小题满分14分)如图所示,某海岛上一观察哨A在上午11时测得一轮船在海岛北偏东 的C处,12时20分测得船在海岛北偏西
的C处,12时20分测得船在海岛北偏西 的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
(本小题满分14分)等比数列 的各项均为正数,且
的各项均为正数,且
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 求数列
求数列 的前n项和
的前n项和 ;
;
(III)设 ,求证:
,求证:
(本小题满分12分)已知 三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
(Ⅰ)若 ,求c的值;
,求c的值;
(Ⅱ)若c=5,求sin∠A的值.
(本小题满分12分)
(Ⅰ)求以下不等式的解集:
(1)  (2)
(2) 
(Ⅱ)若关于x的不等式 的解集为
的解集为 ,求实数m的值.
,求实数m的值.
(本小题满分12分)已知f(x)=ax2(a∈R), g(x)="2lnx."
(1)讨论函数F(x)=f(x)-g(x)的单调性;
(2)是否存在实数a,使得f(x)≥g(x)+2 (x>0)恒成立,若不存在,请说明理由;若存在,求出a的取值范围;
(3)若方程f(x)=g(x)在区间 上有两个不相等的实数根,求a的取值范围.
上有两个不相等的实数根,求a的取值范围.