(本小题满分10分)在直角坐标系 中,以原点
中,以原点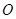 为极点,
为极点,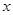 轴的正半轴为极轴,建立极坐标系.已知曲线
轴的正半轴为极轴,建立极坐标系.已知曲线 (
( 为参数),
为参数),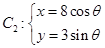 (
(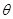 为参数).
为参数).
(Ⅰ)化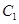 ,
,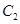 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若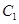 上的点
上的点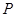 对应的参数为
对应的参数为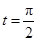 ,
,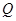 为
为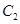 上的动点,求
上的动点,求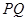 中点
中点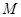 到直线
到直线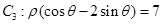 距离的最小值.
距离的最小值.
已知函数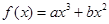 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直,
垂直,
(1)求实数a、b的值;
(2)若函数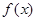 在区间[m,m+1]上单调递增,求m的取值范围.
在区间[m,m+1]上单调递增,求m的取值范围.
.已知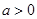 ,设p:函数
,设p:函数 在R上单调递减;命题q:方程
在R上单调递减;命题q:方程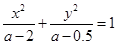 表示的曲线是双曲线,如果“p
表示的曲线是双曲线,如果“p q”为真,“p
q”为真,“p q”为假,求
q”为假,求 的取值范围.
的取值范围.
一个包装箱内有5件产品,其中3件正品,2件次品。现随机抽出两件产品,
(1)求恰好有一件次品的概率。
(2)求都是正品的概率。
(3)求抽到次品的概率。
已知椭圆 上一点
上一点 到它的左右两个焦点的距离和是6,
到它的左右两个焦点的距离和是6,
(1)求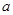 及椭圆离心率的值.
及椭圆离心率的值.
(2)若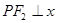 轴(
轴(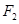 为右焦点),且
为右焦点),且 在
在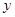 轴上的射影为点
轴上的射影为点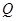 ,求点
,求点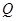 的坐标.
的坐标.
、(本小题满分14 分)已知:数列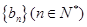 是递增的等比数列,且
是递增的等比数列,且 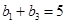 ,
,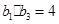
(1)求数列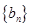 的通项公式;
的通项公式;
(2)若 ,求证数列
,求证数列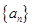 是等差数列;
是等差数列;
(3)求数列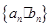 前
前 项和为
项和为