为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前 次考试的数学成绩
次考试的数学成绩 、物理成绩
、物理成绩 进行分析.下面是该生
进行分析.下面是该生 次考试的成绩.
次考试的成绩.
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的理由;
(2)已知该生的物理成绩 与数学成绩
与数学成绩 是线性相关的,若该生的物理成绩达到
是线性相关的,若该生的物理成绩达到 分,请你估计他的数学成绩大约是多少?
分,请你估计他的数学成绩大约是多少?
(已知88 94+83
94+83 91+117
91+117 108+92
108+92 96+108
96+108 104+100
104+100 101+112
101+112 106=70497,
106=70497, )
)
(参考公式: ,
, )
)
(本题满分12分)
已知数列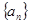 的前
的前 项和,
项和,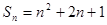 。
。
(I)求数列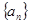 的通项公式
的通项公式 ;
;
(II)记 ,求
,求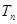 .
.
(本小题满分12分)
一圆与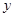 轴相切,圆心在直线
轴相切,圆心在直线 上,在
上,在 上截得的弦长为
上截得的弦长为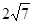 ,
,
求圆的方程。
已知函数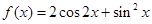
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值和最小值.
的最大值和最小值.
(14分)设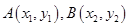 是椭圆
是椭圆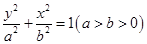 的两点,
的两点,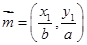 ,
,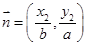 ,且
,且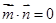 ,椭圆离心率
,椭圆离心率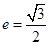 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1) 求椭圆方程;
(2) 若存在斜率为 的直线AB过椭圆的焦点
的直线AB过椭圆的焦点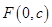 (
(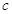 为半焦距),求
为半焦距),求 的值;
的值;
(3) 试问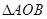 的面积是否为定值?若是,求出该定值;若不是,
的面积是否为定值?若是,求出该定值;若不是, 说明理由。
说明理由。
(13分)已知数列{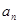 }的前n项和Sn=-
}的前n项和Sn=-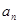 -
-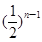 +2(n为正整数).
+2(n为正整数).
(1)令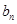 =
=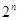
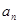 ,求证数列{
,求证数列{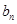 }是等差数列,并求数列{
}是等差数列,并求数列{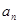 }的通项公式;
}的通项公式;
(2)令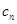 =
=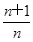
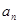 ,若Tn=c1+c2+…+cn, 求Tn。
,若Tn=c1+c2+…+cn, 求Tn。