如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据:sin38°≈0.62,cos38°≈0.79,sin22°≈0.37,cos22°≈0.93,sin37°≈0.60,cos37°≈0.80)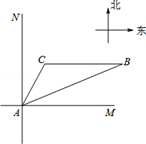
已知:如图,正比例函数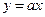 的图象与反比例函数
的图象与反比例函数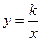 的图象交于点
的图象交于点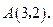
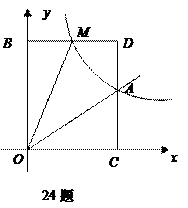
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?
(3)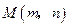 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中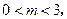 过点
过点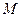 作直线
作直线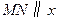 轴,交
轴,交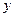 轴于点
轴于点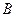 ;过点
;过点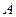 作直线
作直线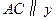
 轴交
轴交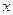 轴于点
轴于点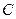 ,交直线
,交直线 于点
于点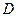 .当四边形
.当四边形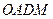 的面积为6时,请判断线段
的面积为6时,请判断线段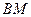 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
|
|
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
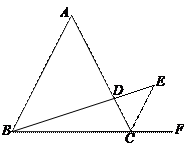
 △ABD∽△CED.
△ABD∽△CED.
如图,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1km,B村到公路l的距离BD=2km,B村在A村的南偏东45°方向上.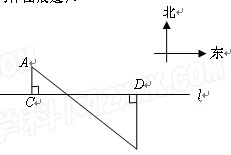
(1)求出A,B两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置(不写作法,保留清晰的作图痕迹).
有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的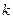 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字 记作一次函数表达式中的
记作一次函数表达式中的 .
.
(1)写出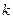 为负数的概率;
为负数的概率;
(2)求一次函数 的图象经过二、三、四象限的概率.(用树状图或列表法求解)
的图象经过二、三、四象限的概率.(用树状图或列表法求解)
如图所示,正方形网格中,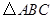 为格点三角形(即三角形的顶点都在格点上).
为格点三角形(即三角形的顶点都在格点上).
(1)把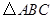 沿
沿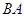 方向平移后,点
方向平移后,点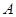 移到点
移到点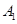 ,在网格中画出平移后得到的
,在网格中画出平移后得到的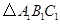 ;
;
(2)把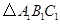 绕点
绕点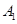 按逆时针方向旋转
按逆时针方向旋转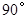 ,在网格中画出旋转后的
,在网格中画出旋转后的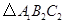 ;
;
(3)如果网格中小正方形的边长为1,求点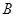 经过(1)、(2)变换的路径总长.
经过(1)、(2)变换的路径总长.